
三、解答题(本大题有5道小题,各小题12分,共60分)
17.在 中,
中, 分别是角
分别是角 的对边,向量
的对边,向量 ,
,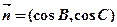 ,且
,且 .
.
(1)求角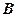 的大小;
的大小;
(2)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在
在
区间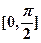 上的最大值和最小值.
上的最大值和最小值.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积. (本题满分12分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(10分)
如图,要计算西湖岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取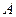 和
和 两点,现测得
两点,现测得 ,
,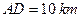 ,
,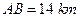 ,
, ,
, ,求两景点
,求两景点 与
与 的距离(精确到0.1km).参考数据:
的距离(精确到0.1km).参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图1,渔船甲位于岛屿 的南偏西
的南偏西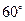 方向的
方向的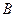 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从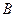 处出发沿北偏东
处出发沿北偏东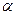 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度;
(2)求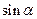 的值.
的值.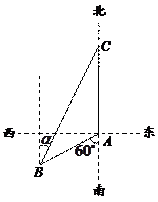
 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
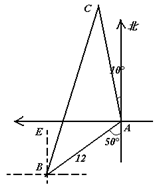
我缉私巡逻艇在一小岛A南偏西50º的方向,距小岛12海里的B处,发现隐藏在小岛边上的一走私船正开始向岛北偏西 10º方向行驶,测得其速度为每小时10海里,问我巡逻艇须用多大的速度朝什么方向航行才能恰在两小时后截获该走私船?(必要时,可参考下列数据sin38º≈0.62,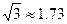 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com