
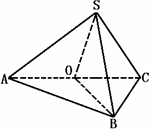
在三棱锥S-ABC中,∠ASB=∠BSC=60°,∠ASC=90°,且SA=SB=SC,求证:平面ASC⊥平面ABC.
|
证明:取AC的中点O,连SO、BO,由已知,得ΔSAB、ΔSBC都是正三角形.∴BC=AB=a,SA=SC=a,又SO⊥AC,BO⊥AC,∴∠SOB就是二面角S-AC-B的平面角.又∵SA=AB=a,SC=BC=a,AC=AC,∴ΔACS≌ΔACB. ∴SO=BO= 即平面SAC⊥平面ABC. 另证:过S作SO⊥平面ABC,垂足是O.∵SA=SB=SC,∴S在平面内的射影是ΔABC的外心,同前面的证明,可知ΔABC是直角三角形,∴O在斜边AC上.又∵平面SAC经过SO,∴平面SAC⊥平面ABC 说明:证明“面面垂直”的常用方法是根据定义证明平面角是90°,或利用判定定理证明一个平面经过另一个平面的垂线. |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:2015届吉林省高一上学期期末考试文科数学试卷(解析版) 题型:选择题
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )

A.相交 B.平行 C.异面 D.以上都有可能
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高考模拟冲刺(提优)测试二理科数学试卷(解析版) 题型:填空题
在三棱锥S-ABC中,△ABC为正三角形,且A在面SBC上的射影H是△SBC的垂心,又二面角H-AB-C为300,则 ;
;
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二上期中文科数学试卷(解析版) 题型:解答题
(本小题满分13分)
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.

(Ⅰ)求证:AD⊥平面SBC;
(Ⅱ)试在SB上找一点E,使得平面ABS⊥平面ADE,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2013届贵州高二下学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.
(I)求证:AD⊥平面SBC;
(II)试在SB上找一点E,使得BC//平面ADE,并证明你的结论.

查看答案和解析>>
科目:高中数学 来源:2014届湖南师大附中高一下学期段考数学试卷(解析版) 题型:解答题
如图,在三棱锥S-ABC中,∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC.
(Ⅰ)证明:平面SBC⊥平面SAB;
(Ⅱ)求二面角A-SC-B的平面角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com