
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)通过讨论a的范围,求出函数f(x)在(0,a]的最大值即可.
解答 解:(Ⅰ)∵f(x)=lnx-x2+x+2,其定义域为(0,+∞),
∴f′(x)=$\frac{-(2x+1)(x-1)}{x}$,
∵x>0,∴当0<x<1时,f′(x)>0;当x>1时,f′(x)<0,
故函数f(x)的单调递增区间是(0,1);单调递减区间是(1,+∞).
(Ⅱ)由(Ⅰ)知,函数f(x)的单调递增区间是(0,1);单调递减区间是(1,+∞),
当0<a≤1时,f(x)在区间(0,a]上单调递增,f(x)的最大值是f(a)=lna-a2+a+2;
当a>1时,f(x)在区间(0,1)上单调递增,在(1,a)上单调递减,
则f(x)在x=1处取得极大值,也即该函数在(0,a]上的最大值,此时f(x)的最大值是f(1)=2;
∴f(x)在区间(0,a]上的最大值f(a)=$\left\{\begin{array}{l}{lna{-a}^{2}+a+2,0<a≤1}\\{2,a>1}\end{array}\right.$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
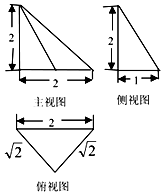
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
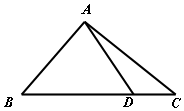 如图,已知D是△ABC边BC上一点.
如图,已知D是△ABC边BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加书法班 | 未参加书法班 | |
| 参加演讲班 | 8 | 5 |
| 未参加演讲班 | 2 | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
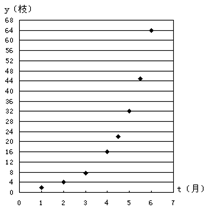 如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )
如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )| A. | 二次函数:y=2t2 | B. | 幂函数:y=t3 | ||
| C. | 指数函数:y=2t | D. | 对数函数:y=log2t |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [2,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com