
思路:反证法是一种间接证法,它先是提出一个与命题的结论相反的假设,然后从这个假设出发,经过正确的推理,导致矛盾,从而否定原假设,达到肯定原命题正确的一种方法.
探究:反设是反证法的基础,为了正确地作出反设,掌握一些常用的互为否定的表述形式是有必要的,例如:是/不是;存在/不存在;平行于/不平行于;垂直于/不垂直于;等于/不等于;大(小)于/不大(小)于;都是不都是;至少有一个一个也没有;至少有n个至多有(n-1)个;至多有一个至少有两个;唯一至少有两个.
归谬是反证法的关键,导出矛盾的过程没有固定的模式,但必须从反设出发,否则推导将成为无源之水,无本之木.推理必须严谨.导出的矛盾有如下几种类型:与已知条件矛盾,与已知的公理、定义、定理、公式矛盾,与反设矛盾,自相矛盾.
反证法可以分为归谬反证法(结论的反面只有一种)与穷举反证法(结论的反面不止一种),如在上述定理证明中,假设点D不在圆上,则有点D在圆外和点D在圆内两种情况,必须一一证出这两种情况都不成立后,才能肯定点D在圆上.
用反证法证明一个命题的步骤,大体上分为:(1)反设;(2)归谬;(3)结论.
对于一些从正面难以说明的问题,反证法往往有着出奇制胜的作用.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:选修设计数学A4-1人教版 人教版 题型:022
圆内接四边形的判定定理.
(1)定理:如果一个四边形的对角________,那么这个四边形的四个顶点共圆.
(2)符号语言表述:在四边形ABCD中,如果∠B+∠D=________或∠A+∠C=180°,那么四边形ABCD内接于圆.
查看答案和解析>>
科目:高中数学 来源:选修设计数学A4-1人教版 人教版 题型:047
圆内接四边形判定定理的推论的证明..
已知:如图,四边形ABCD,延长AB到E,∠EBC=∠CDA.
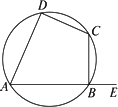
求证:A、B、C、D四点共圆.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com