
两条直线分别被三个互相平行的平面所截,求证:被截得的线段成比例.如图,已知平面α∥β∥γ,直线a分别交α、β、γ于A、B、C,直线b分别交α、β、γ于D、E、F.
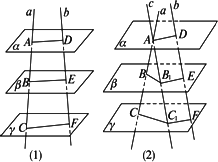
求证:AB∶DE=BC∶EF.
|
解:当a、b共面时,如上图(1),设a、b确定的平面为δ, 则AD、BE、CF分别为α、β、γ与δ的交线. 由α∥β∥γ,知AD∥BE∥CF. 由平行截割定理,知AB∶DE=BC∶EF(当AD、BE、CF中有一条变成一点时,也不影响结果). 当a、b异面时,如上图(2),过A作直线c∥b,分别交β、γ于B1、C1. 由α∥β,知AB1=DE. 同理B1C1=EF. 设a、c确定的平面为δ,则BB1、CC1分别是δ与β、γ的交线. 由β∥γ,知BB1∥CC1. 由平行截割定理,知AB∶AB1=BC∶B1C1. 已知AB1=DE,B1C1=EF,故AB∶DE=BC∶EF. 方法归纳:空间问题应转化为平面问题解决,线段成比例一般考虑平行截割定理.此题也可以连结AF,交平面β于M,将其转化为平面问题解决. |
|
本命题是由平行截割定理扩展来的,因此想到转化为平行截割定理去证.由条件知三个平面互相平行,但原题中没有平面与它们相交,需作出与它们相交的平面.被截的两直线可能异面,也可能共面,所以需分类讨论. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a、b是不重合的两条直线,α、β,γ是三个两两不重合的平面,给出下列四个命题:
①若a⊥α,a⊥β,则α∥β;
②若α⊥γ,β⊥γ,则α∥β;
③若α∥β,![]() ,
, ![]() ,则a∥b;
,则a∥b;
④若α∥β,α∩γ=a,β∩γ=b,则a∥b.
其中正确的是( )
A.①② B.①③ C.③④ D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
![]() 、
、![]() 、
、![]() 是三个平面,a、b 是两条直线,有下列三个条件:
是三个平面,a、b 是两条直线,有下列三个条件:
①a ∥![]() ,b⊂
,b⊂![]() ②a ∥
②a ∥![]() ,b∥
,b∥![]() ③b∥
③b∥![]() ,a⊂
,a⊂![]() .如果命题“
.如果命题“![]() ∩
∩![]() =a, b⊂
=a, b⊂![]() ,且 ________ , 则 a∥b”为真命题, 则可以在横线处填入的条件是 ( )
,且 ________ , 则 a∥b”为真命题, 则可以在横线处填入的条件是 ( )
(A)①或② (B)②或③ (C)①或③ (D)②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com