
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()
【答案】
(1)解:由等高条形图得:
喜欢旅游的女性人数为 ![]() ,不喜欢旅游的女性人数为
,不喜欢旅游的女性人数为 ![]() ;喜欢旅游和不喜欢旅游的男性人数均为
;喜欢旅游和不喜欢旅游的男性人数均为 ![]() .则对应的
.则对应的 ![]() 列联表为:
列联表为:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 |
|
|
|
男性 |
|
|
|
合计 |
|
|
|
(2)解: ![]() 的观测值
的观测值 ![]() 不能在犯错误概率不超过
不能在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”
的前提下认为“喜欢旅游与性别有关”
【解析】(1)根据题意结合所给的数据可得喜欢旅游的女性人数为35,不喜欢旅游的女性人数为15;喜欢旅游和不喜欢旅游的男性人数均为25由此即可求得列表内的值。(2)结合(1)的结论计算可得K2 的观测值,利用该值与标准值的大小关系可得出不能在犯错误概率不超过0.025的前提下认为“喜欢旅游与性别有关”即的结果。
【考点精析】解答此题的关键在于理解用样本的频率分布估计总体分布的相关知识,掌握样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚的看到整个样本数据的频率分布情况,并由此估计总体的分布情况.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1 , C2的极坐标方程分别为ρ=2cosθ, ![]() ,射线θ=φ,
,射线θ=φ, ![]() ,
, ![]() 与曲线C1交于(不包括极点O)三点A,B,C.
与曲线C1交于(不包括极点O)三点A,B,C.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)当 ![]() 时,求点B到曲线C2上的点的距离的最小值.
时,求点B到曲线C2上的点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无穷数列![]() 中,
中, ![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
, ![]() .设
.设![]() ,记使得
,记使得![]() 成立的n的最大值为
成立的n的最大值为![]() .
.
(Ⅰ)设数列{an}为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{an}为等比数列,且a2=2,求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,求出所有可能的数列{an}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.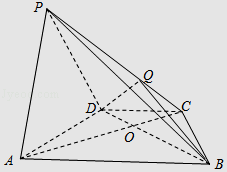
(1)求证:PA∥平面QBD;
(2)求证BD⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A.甲丙丁戊乙
B.甲丁丙乙戊
C.甲乙丙丁戊
D.甲丙戊乙丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点P(0,1)在圆C:x2+y2+2mx﹣2y+m2﹣4m+1=0内,若存在过点P的直线交圆C于A、B两点,且△PBC的面积是△PAC的面积的2倍,则实数m的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2eax .
(Ⅰ)当a<0时,讨论函数f(x)的单调性;
(Ⅱ)在(1)条件下,求函数f(x)在区间[0,1]上的最大值;
(Ⅲ)设函数g(x)=2ex﹣ ![]() ,求证:当a=1,对x∈(0,1),g(x)﹣xf(x)>2恒成立.
,求证:当a=1,对x∈(0,1),g(x)﹣xf(x)>2恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com