
 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题.
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题.分析 (Ⅰ)利用频率分布直方图能求出分数在[120,130)内的频率.
(Ⅱ)由频率分布直方图能估计本次考试的中位数.
(Ⅲ)[110,120)分数段的人数为9人,在[120,130)分数段的人数为18人,用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,需在[110,120)分数段内抽取两人,在[120,130)分数段内抽取4 人,由此能求出至多有1人在分数段[120,130)内的概率.
解答 解:(Ⅰ)分数在[120,130)内的频率为:
1-(0.01+0.015+0.025+0.005)×10=0.3,
∴数学分数恰在[120,130)内的频率为0.3.
(Ⅱ)由频率分布直方图估计本次考试的中位数为:
$\frac{0.5-0.1-0.15-0.15}{0.3}×10+120$=$\frac{370}{3}$.
(Ⅲ)由题意[110,120)分数段的人数为60×0.15=9人,
在[120,130)分数段的人数为60×0.3=18人,
∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,
∴需在[110,120)分数段内抽取两人,并分别记为m,n,
在[120,130)分数段内抽取4 人,并分别记为a,b,c,d,
设“从样本中任取2人,至多有1人在分数在[120,130)内”为事件A,
则基本事件共有:n=${C}_{6}^{2}=15$个,
则事件A包含的基本事件个数m=15-${C}_{4}^{2}$=9个,
∴至多有1人在分数段[120,130)内的概率P(A)=$\frac{m}{n}$=$\frac{9}{15}=\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | λ+μ=2 | B. | λ-μ=1 | C. | λμ=-1 | D. | λμ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
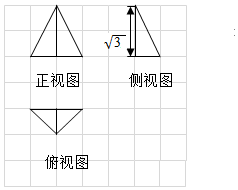 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com