
函数 的部分图象如下图所示,将
的部分图象如下图所示,将 的图象向右平移
的图象向右平移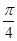 个单位后得到函数
个单位后得到函数 的图象.
的图象.

(1)求函数 的解析式;
的解析式;
(2) 若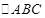 的三边为
的三边为 成单调递增等差数列,且
成单调递增等差数列,且 ,求
,求 的值.
的值.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)对称中心到相邻对称轴的距离等于四分之和个周期,所以 ,由此可得
,由此可得 .再将点
.再将点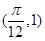 代入
代入 便可求得
便可求得 ,这样便得
,这样便得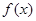 的解析式.再将
的解析式.再将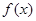 中的
中的 换成
换成 便得
便得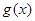 的解析式.
的解析式.
(2)由(1)得 .由
.由 可求出
可求出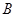 .
.
 成等差,所以
成等差,所以 …………①
…………①
如何利用等式①求 的值?
的值?
注意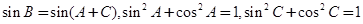 ,所以可令
,所以可令 ……②
……②
①②两式平方相加即可.
试题解析:(1)由图知: ,∵
,∵ ,
,
∴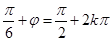 ,即
,即 , 由于
, 由于 ,所以
,所以 ,
, ,函数
,函数 的解析式为
的解析式为 .
.
(2) ,且
,且 ,所以
,所以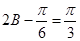 ,
,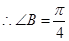 .
.
 成等差,所以
成等差,所以 ,………………………………①
,………………………………①
令 ,………………………………………………………②
,………………………………………………………②
两式平方相加得: ,
,
整理化简得: .由于
.由于 ,所以
,所以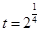 .
.
考点:1、三角函数的图象及其变换;2、正弦定理及三角恒等变换.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年福建安溪一中、养正中学高三上学期期中联考理数学试卷(解析版) 题型:解答题
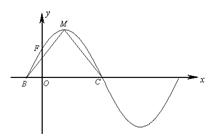
(本小题满分13分)函数
 的部分图象如下图所示,该图象与
的部分图象如下图所示,该图象与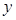 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, 为最高点,且
为最高点,且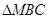 的面积为
的面积为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ) ,求
,求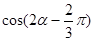 的值.
的值.
(Ⅲ)将函数 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的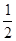 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移 个单位,得函数
个单位,得函数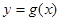 的图象,若函数
的图象,若函数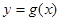 为奇函数,求
为奇函数,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2014届四川省巴中市四县中高一上学期期末考试数学(解析版) 题型:解答题
(12分)已知函数
的部分图象如下图所示。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)若不等式 在
在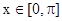 上[来源:Z.xx.k.Com]
上[来源:Z.xx.k.Com]
恒成立,求实数m的取值范围。
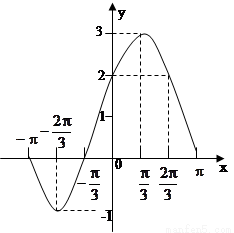
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com