
【题目】如图所示,已知正方体ABCD-A1B1C1D1的棱长为a , 过点B1作B1E⊥BD1于点E , 求A、E两点之间的距离.
【答案】解:以D为坐标原点建立如图所示的空间直角坐标系,
根据题意,可得A(a,0,0)、B(a,a,0)、D1(0,0,a)、B1(a,a,a).
过点E作EF⊥BD于F,如图所示,
则在Rt△BB1D1中,
|BB1|=a,|BD1|= ![]() a,|B1D1|=
a,|B1D1|= ![]() a,
a,
所以|B1E|= ![]() ,
,
所以Rt△BEB1中,|BE|= ![]() a
a
由Rt△BEF∽Rt△BD1D,得|BF|= ![]() a,|EF|=
a,|EF|= ![]() ,所以点F的坐标为(
,所以点F的坐标为( ![]() ,0),
,0),
则点E的坐标为( ![]() ,
, ![]() ).
).
由两点间的距离公式,得
|AE|= ![]() =
= ![]() a,
a,
所以A、E两点之间的距离是 ![]() a.
a.
【解析】先建立适当的直角坐标系,根据题意表示出相关点的坐标,再根据题中点E的位置关系求得点E的坐标,利用两点间的距离公式表示出线段AE的长度.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)的定义域是(0,+∞),f'(x)为f(x)的导函数,且满足f(x)<f'(x),则不等式 ![]() f(2)的解集是( )
f(2)的解集是( )
A.(﹣∞,2)∪(1,+∞)
B.(﹣2,1)
C.(﹣∞,﹣1)∪(2,+∞)
D.(﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
(3)设a>0,若对任意t∈[ ![]() ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆O: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,﹣
,﹣ ![]() ),A(x0 , y0)(x0y0≠0),其上顶点到直线
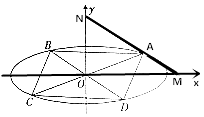
),A(x0 , y0)(x0y0≠0),其上顶点到直线 ![]() x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且
x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且 ![]() =2
=2 ![]() .
. 
(1)证明:|MN|为定值;
(2)如图所示,若A,C关于原点对称,B,D关于原点对称,且 ![]() =λ
=λ ![]() ,求四边形ABCD面积的最大值.
,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应市场需要,某地准备建一个圆形生猪储备基地(如右图),它的附近有一条公路,从基地中心O处向东走1 km是储备基地的边界上的点A , 接着向东再走7 km到达公路上的点B;从基地中心O向正北走8 km到达公路的另一点C.现准备在储备基地的边界上选一点D , 修建一条由D通往公路BC的专用线DE , 求DE的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1的方程为x2+(y+1)2=4,圆O2的圆心为O2(2,1).
(1)若圆O1与圆O2外切,求圆O2的方程;
(2)若圆O1与圆O2交于A , B两点,且|AB|=2 ![]() ,求圆O2的方程.
,求圆O2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4sinxcos(x+ ![]() )+m(x∈R,m为常数),其最大值为2. (Ⅰ)求实数m的值;
)+m(x∈R,m为常数),其最大值为2. (Ⅰ)求实数m的值;
(Ⅱ)若f(α)=﹣ ![]() (﹣
(﹣ ![]() <α<0),求cos2α的值.
<α<0),求cos2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
参考公式: 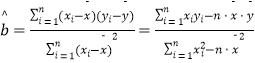 ,
, ![]() .
.
(1)若这两个变量呈线性相关关系,试求y关于x的回归直线方程 ![]() ;
;
(2)已知小王只收购使用年限不超过10年的二手车,且每辆该型号汽车的收购价格为ω=0.03x2﹣1.81x+16.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大? (销售一辆该型号汽车的利润=销售价格﹣收购价格)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com