
【题目】在平面直角坐标系![]() 中,原点为
中,原点为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ,线段
,线段![]() 是抛物线
是抛物线![]() 的一条动弦.
的一条动弦.
(1)求抛物线![]() 的准线方程和焦点坐标
的准线方程和焦点坐标![]() ;
;
(2)当![]() 时,设圆
时,设圆![]() :
:![]() ,若存在两条动弦
,若存在两条动弦![]() ,满足直线
,满足直线![]() 与圆
与圆![]() 相切,求半径
相切,求半径![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,在P地正西方向16km的A处和正东方向2km的B处各一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F.
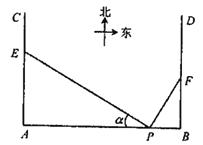
(1)若在P处看E,F的视角![]() ,在B处看E测得
,在B处看E测得![]() ,求AE,BF;
,求AE,BF;
(2)为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]() ,公路PF的毎千米建设成本为a万元,公路PE的毎千米建设成本为8a万元.为节省建设成本,试确定E,F的位置,使公路的总建设成本最小.
,公路PF的毎千米建设成本为a万元,公路PE的毎千米建设成本为8a万元.为节省建设成本,试确定E,F的位置,使公路的总建设成本最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点![]() 的轨迹
的轨迹![]() 的标准方程;
的标准方程;
(2)设动直线![]() 与曲线
与曲线![]() 有且仅有一个公共点,与圆
有且仅有一个公共点,与圆![]() 相交于两点
相交于两点![]() (两点均不在坐标轴上),求直线
(两点均不在坐标轴上),求直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +
+![]() .
.
(1)当m=0时,求不等式f(x)≤9的解集;
(2)当m=2时,若x∈(1,4),f(x) ![]() 2x
2x![]() a<0,求a的取值范围.
a<0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小军的微信朋友圈参与了“微信运动”,他随机选取了40位微信好友(女20人,男20人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别(说明:m~n表示大于等于m,小于等于n):A(0~2000步)1人,B(2001~5000步)2人,C(5001~8000步)3人,D(8001~10000步)6人,E(10001步及以上)8人.若某人一天的走路步数超过8000步被系统认定为“健康型”,否则被系统认定为“进步型”.
(1)请根据选取的样本数据完成下面的![]() 列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
健康型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(2)从小军的40位好友中该天走路步数不超过5000的中随机抽取3人,若![]() 表示抽到的三人分别是x,y,z,试用该表示法列举出试验所有可能的结果.若记“恰好抽到了一位女性好友”为事件A,求事件A的概率.
表示抽到的三人分别是x,y,z,试用该表示法列举出试验所有可能的结果.若记“恰好抽到了一位女性好友”为事件A,求事件A的概率.
附: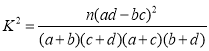 ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为ρ=2cos θ,直线l的参数方程为![]() (t为参数,α为直线的倾斜角).
(t为参数,α为直线的倾斜角).
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C有唯一的公共点,求角α的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com