
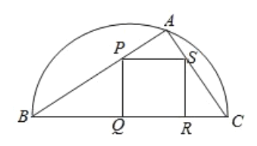
【题目】如图,某园林单位准备绿化一块直径为BC的半圆形空地,![]() 外的地方种草,
外的地方种草,![]() 的内接正方形PQRS为一水池,其余的地方种花.若
的内接正方形PQRS为一水池,其余的地方种花.若![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形PQRS的面积为
,正方形PQRS的面积为![]() .
.
(1)用a,![]() 表示
表示![]() 和
和![]() ;
;
(2)当a为定值,![]() 变化时,求
变化时,求![]() 的最小值,及此时的
的最小值,及此时的![]() 值.
值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),直线C2的方程为
(α为参数),直线C2的方程为![]() ,以O为极点,x轴的正半轴为极轴建立极坐标系.
,以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1和直线C2的极坐标方程;
(2)若直线C2与曲线C1交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,直线 ![]() 的参数方程为
的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)设点P是曲线C上的一个动点,求它到直线![]() 的距离d的取值范围.
的距离d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在R上是增函数,求实数a的取值范围;
在R上是增函数,求实数a的取值范围;
(2)求所有的实数a,使得对任意![]() 时,函数
时,函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的下方;
图象的下方;
(3)若存在![]() ,使得关于x的方程
,使得关于x的方程![]() 有三个不相等的实数根,求实数t的取值范围.
有三个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大衍数列,来源于《乾坤谱》中对易传“大衍之数五十“的推论.主要用于解释中国传统文化中的太极衍生原理数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和是中华传统文化中隐藏着的世界数学史上第一道数列题其规律是:偶数项是序号平方再除以2,奇数项是序号平方减1再除以2,其前10项依次是0,2,4,8,12,18,24,32,40,50,…,如图所示的程序框图是为了得到大衍数列的前100项而设计的,那么在两个判断框中,可以先后填入( )

A. ![]() 是偶数?,
是偶数?,![]() ? B.
? B. ![]() 是奇数?,
是奇数?,![]() ?
?
C. ![]() 是偶数?,
是偶数?, ![]() ? D.
? D. ![]() 是奇数?,
是奇数?,![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技公司新研制生产一种特殊疫苗,为确保疫苗质量,定期进行质量检验.某次检验中,从产品中随机抽取100件作为样本,测量产品质量体系中某项指标值,根据测量结果得到如下频率分布直方图:

(1)求频率分布直方图中![]() 的值;
的值;
(2)技术分析人员认为,本次测量的该产品的质量指标值X服从正态分布![]() ,若同组中的每个数据用该组区间的中间值代替,计算
,若同组中的每个数据用该组区间的中间值代替,计算![]() ,并计算测量数据落在(187.8,212.2)内的概率;
,并计算测量数据落在(187.8,212.2)内的概率;
(3)设生产成本为y元,质量指标值为![]() ,生产成本与质量指标值之间满足函数关系
,生产成本与质量指标值之间满足函数关系![]() 假设同组中的每个数据用该组区间的中间值代替,试计算生产该疫苗的平均成本.
假设同组中的每个数据用该组区间的中间值代替,试计算生产该疫苗的平均成本.
参考数据:![]() ,
,![]()
![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com