
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 过椭圆
过椭圆![]() 的上,下顶点.
的上,下顶点.
(1)求椭圆![]() 的方程.
的方程.
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于点的对称点为
关于点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的
个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的![]() (纵坐标不变)得到函数
(纵坐标不变)得到函数![]() 的图象,关于
的图象,关于![]() 的说法有:①函数
的说法有:①函数![]() 的图象关于点
的图象关于点![]() 对称;②函数
对称;②函数![]() 的图象的一条对称轴是
的图象的一条对称轴是![]() ;③函数
;③函数![]() 在
在![]() 上的最上的最小值为
上的最上的最小值为![]() ;④函数
;④函数![]() 上单调递增,则以上说法正确的个数是( )
上单调递增,则以上说法正确的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为![]() ,
,
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专项规定.某小区采取一系列措施,宣传垃圾分类的知识与意义,并采购分类垃圾箱.为了了解垃圾分类的效果,该小区物业随机抽取了200位居民进行问卷调查,每位居民对小区采取的措施给出“满意”或“不满意”的评价.根据调查结果统计并做出年龄分布条形图和持不满意态度的居民的结构比例图,如图,在这200份问卷中,持满意态度的频率是0.65.
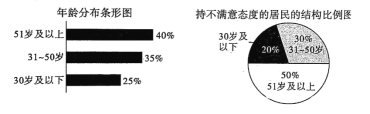
(1)完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
满意 | 不满意 | 总计 | |
51岁及以上的居民 | |||
50岁及以下的居民 | |||
总计 | 200 |
(2)按“51岁及以上”和“50岁及以下”的年龄段采取分层抽样的方法从中随机抽取5份,再从这5份调查问卷中随机抽取2份进行电话家访,求电话家访的两位居民恰好一位年龄在51岁及以上,另一位年龄在50岁及以下的概率.
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附表及参考公式: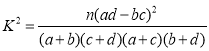 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com