
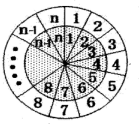
 如图所示的两个同心圆盘均被n等分(n∈N*,n≥2),在相重叠的扇形格中依次同时填上1,2,3,…,n,内圆盘可绕圆心旋转,每次可旋转一个扇形格,格中数之积的和为此位置的“旋转和”.
如图所示的两个同心圆盘均被n等分(n∈N*,n≥2),在相重叠的扇形格中依次同时填上1,2,3,…,n,内圆盘可绕圆心旋转,每次可旋转一个扇形格,格中数之积的和为此位置的“旋转和”.| n+1 |
| 2 |
| n+1 |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n2(n+1)2 |
| 4 |
| n+1 |
| 2 |
| n+1 |
| 2 |
| n+1 |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n2 |
| 4 |
| n(n+2)(5n+2) |
| 24 |
5+
| ||
| 2 |


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
| 1 |
| n |
| n |
| n+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 气温x(℃) | 18 | 13 | 10 | -1 |
| 用电量y(度) | 24 | 24 | 38 | 64 |
 |
| y |
| A、65.5 | B、66.5 |
| C、67.5 | D、68.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、0.49 | B、0.52 |
| C、0.51 | D、0.48 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+3 |
| A、f-1(x)=x2-3(x≤-2) |
| B、f-1(x)=x2-3(x≤0) |
| C、f-1(x)=-x2+3(x≤-2) |
| D、f-1(x)=-x2+3(x≤0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com