
【题目】下面命题正确的是( )
A.“![]() ”是“
”是“![]() ”的 充 分不 必 要条件
”的 充 分不 必 要条件
B.命题“若![]() ,则
,则![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,则
,则![]() ”.
”.
C.设![]() ,则“
,则“![]() 且
且![]() ”是“
”是“![]() ”的必要而不充分条件
”的必要而不充分条件
D.设![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要 不 充 分 条件
”的必要 不 充 分 条件
【答案】ABD
【解析】
选项A:先判断由![]() ,能不能推出
,能不能推出![]() ,再判断由
,再判断由![]() ,能不能推出
,能不能推出![]() ,最后判断本选项是否正确;
,最后判断本选项是否正确;
选项B: 根据命题的否定的定义进行判断即可.
选项C:先判断由![]() 且
且![]() 能不能推出
能不能推出![]() ,然后再判断由
,然后再判断由![]() 能不能推出
能不能推出![]() 且
且![]() ,最后判断本选项是否正确;
,最后判断本选项是否正确;
选项D:先判断由![]() 能不能推出
能不能推出![]() ,再判断由
,再判断由![]() 能不能推出
能不能推出![]() ,最后判断本选项是否正确.
,最后判断本选项是否正确.
选项A:根据反比例函数的性质可知:由![]() ,能推出
,能推出![]() ,但是由
,但是由![]() ,不能推出
,不能推出![]() ,例如当
,例如当![]() 时,符合
时,符合![]() ,但是不符合
,但是不符合![]() ,所以本选项是正确的;
,所以本选项是正确的;
选项B: 根据命题的否定的定义可知:命题“若![]() ,则
,则![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,则
,则![]() ”.所以本选项是正确的;
”.所以本选项是正确的;
选项C:根据不等式的性质可知:由![]() 且
且![]() 能推出
能推出![]() ,本选项是不正确的;
,本选项是不正确的;
选项D: 因为![]() 可以等于零,所以由
可以等于零,所以由![]() 不能推出
不能推出![]() ,再判断由
,再判断由![]() 能不能推出
能不能推出![]() ,最后判断本选项是否正确.
,最后判断本选项是否正确.
故选:ABD


科目:高中数学 来源: 题型:
【题目】已知点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到直线
到直线![]() 的距离相等.
的距离相等.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率为1的直线与曲线
且斜率为1的直线与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个羽毛球协会的运动员人数分别为18,9,18,先采用分层抽样的方法从这三个协会中抽取5名运动员参加比赛.
(1)求应从这三个协会中分别抽取的运动员人数;
(2)将抽取的5名运动员进行编号,编号分别为![]() ,从这5名运动员中随机抽取2名参加双打比赛. 设“编号为
,从这5名运动员中随机抽取2名参加双打比赛. 设“编号为![]() 的两名运动员至少有一人被抽到” 为事件A,求事件A发生的概率.
的两名运动员至少有一人被抽到” 为事件A,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
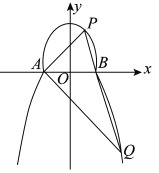
【题目】如图所示,曲线![]() 由部分椭圆
由部分椭圆![]() :
:![]() 和部分抛物线
和部分抛物线![]() :
:![]() 连接而成,
连接而成,![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,其中
,其中![]() 所在椭圆的离心率为
所在椭圆的离心率为![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() 中任意两点均不重合),若
中任意两点均不重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.
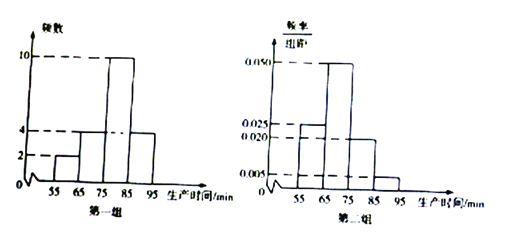
![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年学雷锋日,某中学计划从高中三个年级选派4名教师和若干名学生去当学雷锋文明交通宣传志愿者,用分层抽样法从高中三个年级的相关人员中抽取若干人组成文明交通宣传小组,学生的选派情况如下:
年级 | 相关人数 | 抽取人数 |
高一 | 99 |
|
高二 | 27 |
|
高三 | 18 | 2 |
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)若从选派的高一、高二、高三年级学生中抽取3人参加文明交通宣传,求他们中恰好有1人是高三年级学生的概率;
(Ⅲ)若4名教师可去![]() 、
、![]() 、
、![]() 三个学雷锋文明交通宣传点进行文明交通宣传,其中每名教师去
三个学雷锋文明交通宣传点进行文明交通宣传,其中每名教师去![]() 、
、![]() 、
、![]() 三个文明交通宣传点是等可能的,且各位教师的选择相互独立.记到文明交通宣传点
三个文明交通宣传点是等可能的,且各位教师的选择相互独立.记到文明交通宣传点![]() 的人数为
的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com