
【题目】已知椭圆 C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,右焦点为
,右焦点为![]() .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为![]() ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
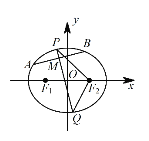
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用椭圆C:![]() (a>b>0)的焦距为2,且过点(1,
(a>b>0)的焦距为2,且过点(1,![]() ),建立方程组,求出a,b,即可求椭圆C的方程;
),建立方程组,求出a,b,即可求椭圆C的方程;
(2)分类讨论,求出直线PQ的方程,与椭圆方程联立,结合向量的数量积,![]() 在椭圆的内部,利用换元法,即可求
在椭圆的内部,利用换元法,即可求![]() 的取值范围.
的取值范围.
(1) 因为椭圆 ![]() 的焦距为
的焦距为 ![]() ,且过点K
,且过点K ![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,于是
,于是 ![]() ,
,![]() ,所以椭圆
,所以椭圆 ![]() 的方程为
的方程为 ![]() .
.
(2) 由题意,当直线 ![]() 垂直于
垂直于 ![]() 轴时,直线
轴时,直线 ![]() 方程为
方程为 ![]() ,此时
,此时 ![]() ,
,![]() ,得
,得 ![]() .
.
当直线 ![]() 不垂直于
不垂直于 ![]() 轴时,设直线
轴时,设直线 ![]() 的斜率为
的斜率为 ![]() ,
,![]() ,
,![]() ,
,![]() ,由线段
,由线段 ![]() 的中点
的中点 ![]() 的横坐标为
的横坐标为 ![]() ,得
,得 ![]() ,则
,则 ![]() ,故
,故 ![]() .此时,直线
.此时,直线 ![]() 斜率为
斜率为 ![]() ,
,![]() 的直线方程为
的直线方程为 ![]() ,即
,即 ![]() .联立
.联立 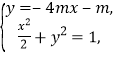 消去
消去 ![]() ,整理得
,整理得 ![]() .设
.设 ![]() ,
,![]() ,所以
,所以 ![]() ,
,![]() ,
,
于是 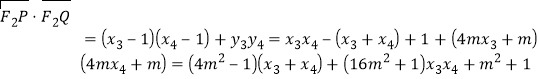
![]()
![]()
由于 ![]() 在椭圆的内部,故
在椭圆的内部,故 ![]() ,令
,令 ![]() ,
,![]() ,
,
则 ![]() .又
.又 ![]() ,所以
,所以 ![]() .综上,
.综上,![]() 的取值范围为
的取值范围为 ![]() .
.


科目:高中数学 来源: 题型:
【题目】在某海礁A处有一风暴中心,距离风暴中心A正东方向200km的B处有一艘轮船,正以北偏西a(a为锐角)角方向航行,速度为40km/h.已知距离风暴中心180km以内的水域受其影响.
(1)若轮船不被风暴影响,求角α的正切值的最大值?
(2)若轮船航行方向为北偏西45°,求轮船被风暴影响持续多少时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
=1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
(I) 求证;直线 ![]() =1是椭圆C在点P处的切线;
=1是椭圆C在点P处的切线;
(Ⅱ)求证: ![]() 为定值,并求此定值;
为定值,并求此定值;
(Ⅲ)请问△ONP(O为坐标原点)的面积是否存在最小值?若存在,请求出最小及此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 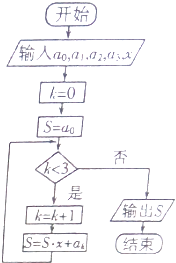
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48. 
(1)求an1和a4n;
(2)设bn= ![]() +(﹣1)na
+(﹣1)na ![]() (n∈N+),求数列{bn}的前n项和Sn .
(n∈N+),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx(ω>0),将y=f(x)的图象向右平移 ![]() 个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求证:AC⊥PB;
(2)若PB=PC= ![]() ,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为
,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com