
(本题满分12分)设正项数列 的前
的前 项和
项和 ,且满足
,且满足 .
.
(Ⅰ)计算 的值,猜想
的值,猜想 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)设 是数列
是数列 的前
的前 项和,证明:
项和,证明: .
.
(Ⅰ)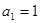 ;
;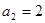 ;
;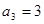 .猜想
.猜想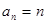 ,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明
,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明
【解析】
试题分析:(Ⅰ)当n=1时,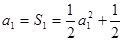 ,得
,得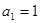 ;
;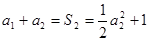 ,得
,得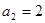 ;
;
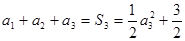 ,得
,得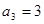 .猜想
.猜想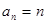 2’
2’
证明:(ⅰ)当n=1时,显然成立.
(ⅱ)假设当n=k时,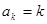 1’
1’
则当n=k+1时,
结合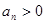 ,解得
,解得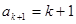 2’
2’
于是对于一切的自然数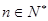 ,都有
,都有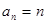 1’
1’
(Ⅱ)证法一:因为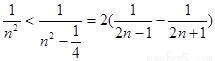 ,
3’
,
3’
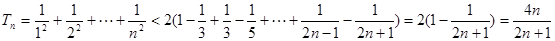 .3’
.3’
证法二:数学归纳法
证明:(ⅰ)当n=1时,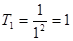 ,
,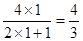 ,
,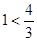 1’
1’
(ⅱ)假设当n=k时,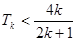 1’
1’
则当n=k+1时,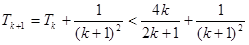
要证: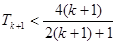
只需证: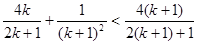
由于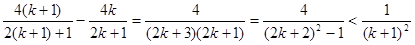
所以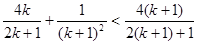 3’
3’
于是对于一切的自然数 ,都有
,都有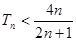 1’
1’
考点:本题考查了数学归纳法的运用
点评:运用数学归纳法,可以证明下列问题:与自然数n有关的恒等式、代数不等式、三角不等式、数列问题、几何问题、整除性问题等等。


科目:高中数学 来源:2014届吉林省吉林市高二上学期期中理科数学试卷(解析版) 题型:解答题
(本题满分12分)
设命题 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 满足
满足 .
.
当 为真,求实数
为真,求实数 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄市高三暑期第二次考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)设函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省高三十一月份阶段性考试理科数学 题型:解答题
(本题满分12分)设函数 ,其中
,其中 。
。
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式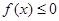 的解集为
的解集为 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年云南省高二上学期期末数学理卷 题型:解答题
(本题满分12分)
设 ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 斜率为1的直线
斜率为1的直线 与
与 相交于
相交于 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列,
(Ⅰ)求 的离心率;
的离心率;
(Ⅱ)设点 满足
满足 ,求
,求 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com