
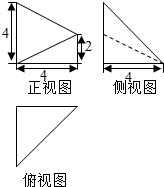
 已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A-BCED的体积为16.将直角三角形△ABD绕斜边AD旋转一周,则BD=2;该旋转体的表面积为$\frac{32+8\sqrt{2}}{3}π$.
已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A-BCED的体积为16.将直角三角形△ABD绕斜边AD旋转一周,则BD=2;该旋转体的表面积为$\frac{32+8\sqrt{2}}{3}π$. 分析 由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=a,利用几何体A-BCED的体积为16,求BD的值;过B作AD的垂线BH,垂足为H,得BH=$\frac{4\sqrt{2}}{3}$,求出圆锥底面周长为C,结合两个圆锥的母线长,即可求该旋转体的表面积.
解答  解:由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=a,
解:由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=a,
体积V=$\frac{1}{3}$•4•$\frac{1}{2}$(a+4)×4=16,
解得a=BD=2;
在RT△ABD中,AB=4$\sqrt{2}$,BD=2,AD=6,
过B作AD的垂线BH,垂足为H,得BH=$\frac{4\sqrt{2}}{3}$,
该旋转体由两个同底的圆锥构成,圆锥底面半径为BH=$\frac{4\sqrt{2}}{3}$,
所以圆锥底面周长为C=2π•$\frac{4\sqrt{2}}{3}$=$\frac{8\sqrt{2}}{3}π$,
两个圆锥的母线长分别为4$\sqrt{2}$和2,
故该旋转体的表面积为S=$\frac{1}{2}$×$\frac{8\sqrt{2}}{3}π$(2+4$\sqrt{2}$)=$\frac{32+8\sqrt{2}}{3}π$.
故答案为:2,$\frac{32+8\sqrt{2}}{3}π$
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图直角梯形OADC中,OA∥CD,∠D=60°,OA=1,CD=2,在梯形内挖去一个以OA为半径的四分之一圆,图中阴影部分绕OC所在直线旋转一周,求该旋转体的体积和表面积.
如图直角梯形OADC中,OA∥CD,∠D=60°,OA=1,CD=2,在梯形内挖去一个以OA为半径的四分之一圆,图中阴影部分绕OC所在直线旋转一周,求该旋转体的体积和表面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2)∪(2,+∞) | B. | (1,2)∪(2,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com