
如图,已知平面四边形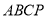 中,
中,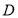 为
为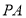 的中点,
的中点,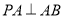 ,
,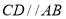 ,
,
且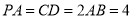 .将此平面四边形
.将此平面四边形 沿
沿 折成直二面角
折成直二面角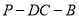 ,
,
连接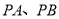 ,设
,设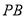 中点为
中点为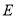 .
.
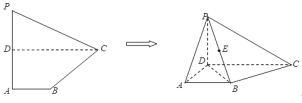
(1)证明:平面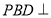 平面
平面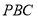 ;
;
(2)在线段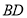 上是否存在一点
上是否存在一点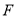 ,使得
,使得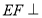 平面
平面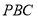 ?若存在,请确定点
?若存在,请确定点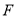 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(3)求直线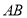 与平面
与平面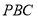 所成角的正弦值.
所成角的正弦值.
(1)详见解析;(2)点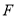 存在,且为线段
存在,且为线段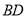 上靠近点
上靠近点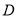 的一个四等分点;(3)
的一个四等分点;(3)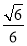 .
.
【解析】
试题分析:(1)分别证明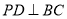 ,
,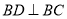 即可;(2)方法一:先以
即可;(2)方法一:先以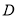 为原点,
为原点,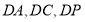 分别为
分别为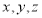 轴,建立直角坐标系,写出各点坐标
轴,建立直角坐标系,写出各点坐标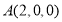 ,
,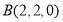 ,
,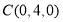 ,
,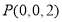 ,
,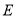 为
为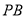 中点,故
中点,故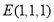 ,设点
,设点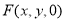 ,利用
,利用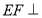 平面
平面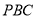 得
得 ,据此可解出
,据此可解出 ;方法二:作
;方法二:作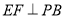 交
交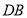 于
于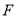 ,注意到
,注意到 ,故
,故 与
与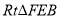 相似,因此
相似,因此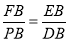 ,于是得
,于是得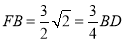 ;(3)方法一:由于
;(3)方法一:由于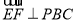 ,即
,即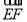 为平面
为平面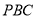 的法向量,
的法向量, ,
,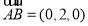 ,要求直线
,要求直线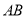 与平面
与平面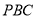 所成角的正弦值,记直线
所成角的正弦值,记直线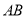 与平面
与平面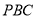 所成角为
所成角为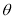 ,根据直线与面的夹角正弦正好等于直线与面的法向量的夹角余弦的绝对值,则知
,根据直线与面的夹角正弦正好等于直线与面的法向量的夹角余弦的绝对值,则知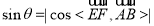 ,故只需计算
,故只需计算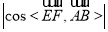 即可,利用余弦公式有
即可,利用余弦公式有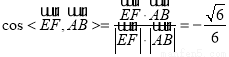 ,故
,故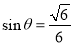 ;方法二:由于
;方法二:由于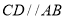 ,所以可以转而考虑
,所以可以转而考虑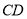 与平面
与平面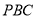 所成角,为此需要找到
所成角,为此需要找到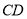 在平面
在平面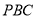 内的投影,此投影与
内的投影,此投影与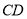 所成角即为线面夹角,然后求
所成角即为线面夹角,然后求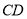 与平面
与平面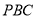 所成角的正弦,于是在
所成角的正弦,于是在 中作
中作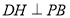 ,而平面
,而平面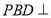 平面
平面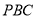 ,由此
,由此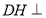 平面
平面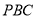 ,
,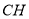 即为
即为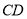 在平面
在平面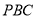 内的投影,
内的投影,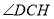 就等于直线
就等于直线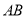 与平面
与平面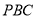 所成角,
所成角, 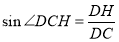 ,
,
在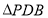 中,
中, ,
,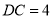 ,
,
故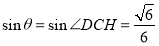 .
.
试题解析:(1)直二面角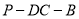 的平面角为
的平面角为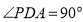 ,又
,又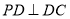 ,
,
则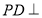 平面
平面 ,所以
,所以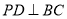 .
.
又在平面四边形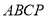 中,由已知数据易得
中,由已知数据易得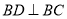 ,而
,而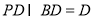 ,
,
故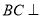 平面
平面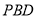 ,因为
,因为 平面
平面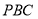 ,所以平面
,所以平面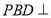 平面
平面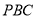 (4分)
(4分)
(2)解法一:由(1)的分析易知, ,则以
,则以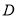 为原点建立空间直角坐标系如图所示.
为原点建立空间直角坐标系如图所示.


结合已知数据可得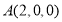 ,
,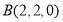 ,
,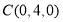 ,
,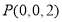 ,
,
则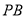 中点
中点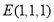 .
.
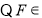 平面
平面 ,故可设
,故可设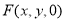 ,
,
则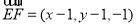 ,
,
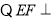 平面
平面 ,
, ,
,
又 ,
,
由此解得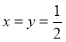 ,即
,即 ,
,
易知这样的点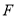 存在,且为线段
存在,且为线段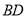 上靠近点
上靠近点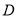 的一个四等分点; (8分)
的一个四等分点; (8分)
解法二:(略解)如图所示,

在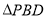 中作
中作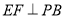 ,交
,交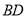 于
于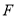 ,
,
因为平面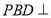 平面
平面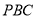 ,则有
,则有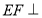 平面
平面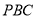 .
.
在 中,结合已知数据,利用三角形相似等知识可以求得
中,结合已知数据,利用三角形相似等知识可以求得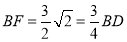 ,
,
故知所求点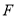 存在,且为线段
存在,且为线段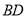 上靠近点
上靠近点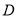 的一个四等分点; ..(8分)
的一个四等分点; ..(8分)
(3)解法一:由(2) 是平面
是平面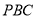 的一个法向量,又
的一个法向量,又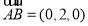 ,
,
则得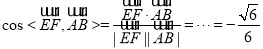 ,所以
,所以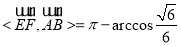 ,
,
记直线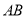 与平面
与平面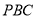 所成角为
所成角为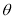 ,则知
,则知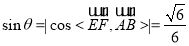 ,
,
故所求角的正弦值为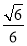 . ..(12分)
. ..(12分)
解法二:(略解)如上图中,因为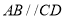 ,所以直线
,所以直线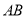 与平面
与平面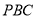 所成角等于直线
所成角等于直线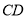 与平面
与平面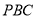 所成角,由此,在
所成角,由此,在 中作
中作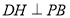 于
于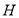 ,易证
,易证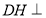 平面
平面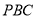 ,
,
连接 ,则
,则 为直线
为直线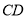 与平面
与平面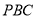 所成角,
所成角,
结合题目数据可求得 ,故所求角的正弦值为
,故所求角的正弦值为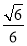 . ..(12分)
. ..(12分)
考点:1、线面垂直、面面垂直的证法;2、线面角的求法;3、空间向量的应用.


科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考理科数学试卷(解析版) 题型:选择题
已知向量a=(sin θ,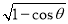 ),b=(1,
),b=(1,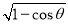 ),其中θ∈
),其中θ∈ ,则一定有 ( )
,则一定有 ( )
A.a∥b B.a⊥b C.a与b的夹角为45° D.|a|=|b|
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试理科数学试卷(解析版) 题型:选择题
用0,1,2,3,4这五个数字组成没有重复数字的五位数中,奇数的个数是( )
(A)24 (B)36 (C)48 (D)72
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:选择题
已知函数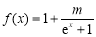 ,若
,若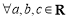 ,
,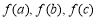 为某一个三角形的边长,则实数m的取值范围是( )
为某一个三角形的边长,则实数m的取值范围是( )
(A)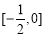 (B)
(B)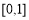 (C)
(C)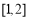 (D)
(D)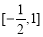
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:选择题
下列说法正确的是( )
(A)“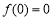 ”是“函数
”是“函数 是奇函数”的充要条件
是奇函数”的充要条件
(B)若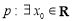 ,
,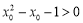 ,则
,则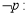
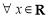 ,
,
(C)若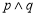 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
(D)“若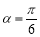 ,则
,则 ”的否命题是“若
”的否命题是“若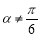 ,则
,则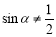 ”
”
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟理科数学试卷(解析版) 题型:选择题
将函数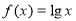 的图象向左平移1个单位,再将位于
的图象向左平移1个单位,再将位于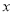 轴下方的图象沿
轴下方的图象沿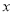 轴翻折得到函数
轴翻折得到函数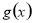 的图象,若实数
的图象,若实数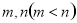 满足
满足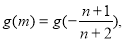
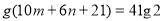 则
则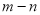 的值是( )
的值是( )
A.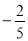 B.
B.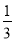 C.
C.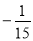 D.
D.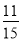
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com