
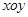 中,设二次函数
中,设二次函数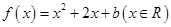 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求: .
. =0,得抛物线与
=0,得抛物线与 轴交点是(0,b);令
轴交点是(0,b);令 ,
,
 ,令y=0,得
,令y=0,得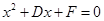 ,
, =0 是同解方程,可得D,F的值,再根据
=0 是同解方程,可得D,F的值,再根据 =0 得
=0 得 =0,此方程有一个根为b,代入得出E=―b―1.从而可求出圆C的方程.
=0,此方程有一个根为b,代入得出E=―b―1.从而可求出圆C的方程. =0,得抛物线与
=0,得抛物线与 轴交点是(0,b);令
轴交点是(0,b);令 ,
,
 ,
, =0 得
=0 得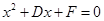 .
. =0 是同一个方程,
=0 是同一个方程, .
. =0 得
=0 得 =0,此方程有一个根为b,代入得出E=―b―1.
=0,此方程有一个根为b,代入得出E=―b―1. .
.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
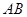 是⊙
是⊙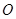 的直径,
的直径,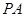 垂直于⊙
垂直于⊙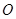 所在的平面,
所在的平面,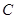 是圆周上不同于
是圆周上不同于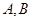 的一动点.
的一动点.
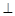 面PBC;
面PBC;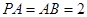 ,则当直线
,则当直线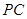 与平面
与平面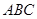 所成角正切值为
所成角正切值为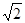 时,求直线
时,求直线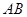 与平面
与平面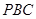 所成角的正弦值.
所成角的正弦值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com