
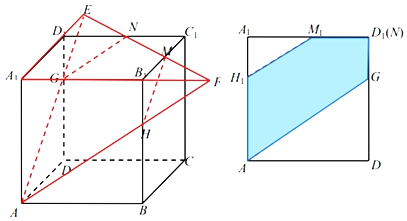
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为_____.
【答案】![]()
【解析】
由图象可得投影为五边形AH1M1D1G,利用三角形相似性质得到DG=2D1G![]() ,BH=2B1H
,BH=2B1H![]() ,进而求得AH1=2A1H1
,进而求得AH1=2A1H1![]() ,A1M1=D1M1
,A1M1=D1M1![]() ,则可得
,则可得![]() 1
1![]() SADG.
SADG.
解:直线MN分别与直线A1D1,A1B1交于E,F两点,
连接AE,AF,分别与棱DD1,BB1交于G,H两点,连接GN,MH,
得到截面五边形AGNMH,
向平面ADD1A1作投影,得到五边形AH1M1D1G,
由点M,N分别是棱B1C1,C1D1的中点,可得D1E=D1N![]() ,
,
由△D1EG∽△DAG,可得DG=2D1G![]() ,
,
同理BH=2B1H![]() ,
,
则AH1=2A1H1![]() ,A1M1=D1M1
,A1M1=D1M1![]() ,
,
则![]() 1
1![]() SADG=1
SADG=1![]() 1
1![]() ,
,

故答案为:![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】在2019年亚洲杯前,某商家为了鼓励中国球迷组团到阿联酋支持中国队,制作了3种精美海报,每份中国队球迷礼包中随机装入一份海报,每集齐3种不同的海报就可获得中国队在亚洲杯上所有比赛中的1张门票.现有6名中国队球迷组成的球迷团,每人各买一份中国队球迷礼包,则该球迷团至少获得1张门票的可能情况的种数为( )
A.360B.450C.540D.990
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线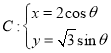 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x|+|x﹣1|.
(1)若f(x)≥|m﹣1|恒成立,求实数m的最大值M;
(2)在(1)成立的条件下,正实数a,b满足a2+b2=M,证明:a+b≥2ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为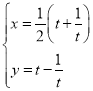 (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系.
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)写出曲线C的普通方程和极坐标方程;
(Ⅱ)M,N为曲线C.上两点,若OM⊥ON,求|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的弦长为3,直线
轴的弦长为3,直线![]() 与圆
与圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为椭圆的右顶点.
为椭圆的右顶点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)用![]() ,
,![]() 分别表示
分别表示![]() 和
和![]() 的面积,求
的面积,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com