
| ai |
| ai |
| ai |
| ai+1 |
| Tm |
| a1 |
| a2 |
| am |
| Tm |
| ai |
| ai |
| ai+1 |
| a1 |
| a2 |
| a2 |
| a3 |
| a3 |
| a4 |
| a1 |
| a3 |
| a2 |
| a4 |
| a1 |
| a4 |
| Tm |
| a1 |
| a2 |
| am |
| a1 |
| a2 |
| a1 |
| a3 |
| am-1 |
| am |
| ai |
| ai |
| ai+1 |
| a1 |
| a2 |
| a2 |
| a3 |
| a3 |
| a4 |
| a1 |
| a3 |
| a2 |
| a4 |
| a1 |
| a4 |
| Tm |
| a1 |
| a2 |
| a4 |
| a1 |
| a2 |
| am |
| a1 |
| a2 |
| a1 |
| a3 |
| am-1 |
| am |
| a1 |
| a2 |
| a1 |
| a3 |
| am-1 |
| am |
| T2 |
| T2 |
| 2 |
| T3 |
| T3 |
| T4 |
| T4 |
| 2 |
| 2 |


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| NP |
| PM |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| Sn |
| n |
| Sn+k |
| Sn-k |
| Sn |
| b1+b2+…+bn |
| n |
| b1+bn |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
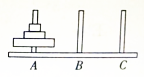 从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.
从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com