
【题目】每年春节,各地的餐馆都出现了用餐需预定的现象,致使一些人在没有预定的情况下难以找到用餐的餐馆,针对这种现象,专家对人们的用餐地点及性别作出调查,得到的情况如下表所示:
在家用餐 | 在餐馆用餐 | 总计 | |
男性 | 30 | ||
女性 | 40 | ||
总计 | 50 | 100 |
(1)完成上述![]() 列联表;
列联表;
(2)根据表中的数据,试通过计算判断是否有![]() 的把握说明用餐地点与性别有关?
的把握说明用餐地点与性别有关?
参考公式及数据: ,其中
,其中![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】以下是我们常见的空间几何体.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(1) (2) (3) (4) (5) (6) (7) (8) (9)(10)
![]()
(11)
(1)以上几何体中哪些是棱柱?
(2)一个几何体为棱柱的充要条件是什么?
(3)如何求以上几何体的表面积?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 上一点与两焦点构成的三角形的周长为
上一点与两焦点构成的三角形的周长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆C的右顶点和上顶点分别为A、B,斜率为![]() 的直线l与椭圆C交于P、Q两点(点P在第一象限).若四边形APBQ面积为
的直线l与椭圆C交于P、Q两点(点P在第一象限).若四边形APBQ面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
A. 3690 B. 3660 C. 1845 D. 1830
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为落实国家“精准扶贫”政策,让市民吃上放心蔬菜,某企业于2018年在其扶贫基地投入![]() 万元研发资金,用于蔬菜的种植及开发,并计划今后十年内在此基础上,每年投入的资金比上一年增长10%.
万元研发资金,用于蔬菜的种植及开发,并计划今后十年内在此基础上,每年投入的资金比上一年增长10%.
(1)写出第![]() 年(2019年为第一年)该企业投入的资金数
年(2019年为第一年)该企业投入的资金数![]() (万元)与
(万元)与![]() 的函数关系式,并指出函数的定义域;
的函数关系式,并指出函数的定义域;
(2)该企业从第几年开始(2019年为第一年),每年投入的资金数将超过![]() 万元?
万元?
(参考数据![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
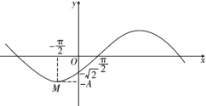
【题目】函数![]() 的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点的坐标为
的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点的坐标为![]() ,与y轴的交点坐标为
,与y轴的交点坐标为![]() .
.
(1)求A,![]() ,
,![]() 的值;
的值;
(2)若关于x的方程![]() 在
在![]() 上有一解,求实数m的取值范围.
上有一解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸线l一侧P处有一个美丽的小岛,某旅游公司为方便登岛游客,在l上设立了M,N两个报名接待点,P,M,N三点满足任意两点间的距离为![]() 公司拟按以下思路运作:先将M,N两处游客分别乘车集中到MN之间的中转点Q处
公司拟按以下思路运作:先将M,N两处游客分别乘车集中到MN之间的中转点Q处![]() 点Q异于M,N两点
点Q异于M,N两点![]() ,然后乘同一艘游轮由Q处前往P岛
,然后乘同一艘游轮由Q处前往P岛![]() 据统计,每批游客报名接待点M处需发车2辆,N处需发车4辆,每辆汽车的运费为20元
据统计,每批游客报名接待点M处需发车2辆,N处需发车4辆,每辆汽车的运费为20元![]() ,游轮的运费为120元
,游轮的运费为120元![]() 设
设![]() ,每批游客从各自报名点到P岛所需的运输总成本为T元.
,每批游客从各自报名点到P岛所需的运输总成本为T元.
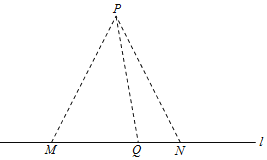
![]() 写出T关于
写出T关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
![]() 问:中转点Q距离M处多远时,T最小?
问:中转点Q距离M处多远时,T最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com