Question

【题目】为了绿化城市，要在矩形区域ABCD内建一个矩形草坪，如图所示，另外，△AEF内部有一文物保护区不能占用，经测量AB＝100 m，BC＝80 m，AE＝30 m，AF＝20 m，应如何设计才能使草坪面积最大？

Answer 1

【答案】见解析．

【解析】试题分析：线段EF的方程是＋＝1(0≤x≤30)．在EF上取点P(m，n)，矩形PQCR的面积为S，则S＝|PR|·|PQ|＝(100－m)(80－n)．结合＋＝1，整理得 S＝－ (m－5)2＋ (0≤m≤30)，求得当m＝5时，S有最大值．

试题解析：由已知得E(30,0)，F(0,20)，则直线EF的方程是＋＝1(0≤x≤30)．如图所示，在EF上取点P(m，n)，作PQ⊥BC于Q，PR⊥CD于R，设矩形PQCR的面积为S，

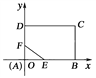
则S＝|PR|·|PQ|＝(100－m)(80－n)．∵＋＝1，∴n＝20(1－)．∴S＝(100－m)(80－20＋m)＝－ (m－5)2＋ (0≤m≤30)，

∴当m＝5时，S有最大值．

点晴：本题考查的是函数模型的应用。解决函数模型应用的解答题，要注意以下几点：①读懂实际背景，将实际问题转化为函数模型．②对涉及的相关公式，记忆要准确．③在求解的过程中计算要正确.另外需要熟练掌握求解方程、不等式、函数最值的方法，才能快速正确地求解．