
【题目】给定平面上的五个点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
A. 120种 B. 125种 C. 130种 D. 135种
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知递增数列{an}前n项和为Sn,且满足a1=3,4Sn﹣4n+1=an2,设bn![]() (n∈N*)且数列{bn}的前n项和为Tn
(n∈N*)且数列{bn}的前n项和为Tn
(Ⅰ)求证:数列{an}为等差数列;
(Ⅱ)若对任意的n∈N*,不等式λTn![]() n
n![]() (﹣1)n+1恒成立,求实数λ的取值范围.
(﹣1)n+1恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列各命题:
①两两相交且不共点的三条直线确定一个平面:
②若真线![]() 不平行于平面
不平行于平面![]() ,则直线
,则直线![]() 与平面
与平面![]() 有公共点:
有公共点:
③若两个平面垂直,则一个平面内的已知直线必垂直于另一个平面的无数条直线:
④若两个二面角的两个面分别对应垂直,则这两个二面角相等或互补.
则其中正确的命题共有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村充分利用自身资源,大力发展养殖业以增加收入.计划共投入80万元,全部用于甲、乙两个项目,要求每个项目至少要投入20万元在对市场进行调研时发现甲项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足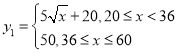 ,乙项目的收益
,乙项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足![]() .
.
(1)当甲项日的投入为25万元时,求甲、乙两个项目的总收益;
(2)问甲、乙两个项目各投入多少万元时,总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求实数k的值;
(2)若![]() ,试判断函数
,试判断函数![]() 的单调性,并求不等式
的单调性,并求不等式![]() 的解集;
的解集;
(3)若![]() ,设
,设![]() ,
,![]() 在
在![]() 上的最小值为-1,求实数m的值.
上的最小值为-1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,AB=2BC=2,E为CD中点,以BE为折痕将△BEC折起,使C到C′的位置,且平面BEC′⊥平面ABED.

(1)求证:BC′⊥AE;
(2)求空间四边形ABC′E的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱椎![]() 中,
中, ![]() 是棱
是棱![]() 上一点,且
上一点,且![]() ,底面
,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 为正三角形,且平面
为正三角形,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
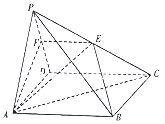
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com