
【题目】在120°的二面角α-![]() -β的两个面内分别有点A,B,A∈α,B∈β,A,B到棱l的距离AC,BD分别是2,4,且线段AB=10.
-β的两个面内分别有点A,B,A∈α,B∈β,A,B到棱l的距离AC,BD分别是2,4,且线段AB=10.
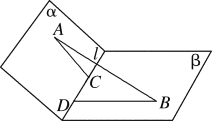
(1)求C,D间的距离;
(2)求直线AB与平面β所成角的正弦值.
【答案】(1)6![]() (2)
(2)![]()
【解析】
(1)要求CD长,应将CD放在三角形中,过点C作BD的平行线,取CE=BD=4,根据余弦定理可求出AE的长,最后在直角三角形AEB求出BE长,而四边形BECD为矩形,即可求出所求;
(2)在△ACD所在的平面内,作AF⊥CD交CD的延长线于点F,利用面面垂直的性质即可证明AF⊥平面Q,从而得到∠ABF是直线AB和平面Q所成的角.
(1)过点C作BD的平行线,取CE=BD=4,
∵AC⊥l,而CE⊥l,则∠ACE=120°
根据余弦定理可知cos∠ACE![]()
解得:AE![]()
而三角形AEB为直角三角形,则BE=6![]()
即CD=6![]()
(2)在△ACE所在的平面内,作AO⊥CE交CE的反向延长线于点O.
∵平面ACE⊥平面β,∴AF⊥平面β.
在△ACO中,∠ACO=60°,AC=2,∴AO![]() .
.
连接OB,于是∠ABO是AB和平面β所成的角,
在△ABO为直角三角形,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】雾霾影响人们的身体健康,越来越多的人开始关心如何少产生雾霾,春节前夕,某市健康协会为了了解公众对“适当甚至不燃放烟花爆竹”的态度,随机采访了50人,将凋查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 12 | 7 | 3 | 3 |
(1)以赞同人数的频率为概率,若再随机采访3人,求至少有1人持赞同态度的概率;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(-x-1)=f(x-1),其图象过点(0,1),且与x轴有唯一交点。
(1)求f(x)的解析式;
(2)设函数g(x)=f(x)-(2+a)x,求g(x)在[1,2]上的最小值h(a)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,C、D是以AB为直径的圆上两点,AB=2AD=2![]() ,AC=BC,F 是AB上一点,且AF=
,AC=BC,F 是AB上一点,且AF=![]() AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知:
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知:![]() ,
, 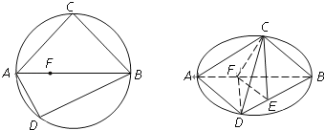
(1)求证:AD⊥平面BCE;
(2)求三棱锥A﹣CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为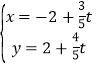 (t为参数),它与曲线
(t为参数),它与曲线
C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是几何体的平面展开图,其中四边形ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面4个结论:
①直线BE与直线CF共面;②直线BE与直线AF异面;
③直线EF∥平面PBC;④平面BCE⊥平面PAD.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com