练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    t∈R，且t∈(0，10)，由t确定两个任意点P(t，t)，Q(10－t，0)．

    (1)问：直线PQ是否能通过下面的点M(6，1)，N(4，5)；

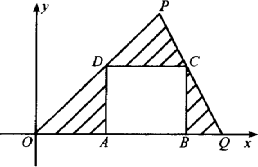
    (2)在△OPQ内作内接正方形ABCD，顶点A、B在边OQ上，顶点C在边PQ上，顶点D在OP上．

    ①求证：顶点C一定在直线y＝x上；

    ②求如图中阴影部分面积的最大值，并求这时顶点A、B、C、D的坐标．

    答案：
    解析：


    提示：

    这是一道结论开放的探索性问题，注意此类问题的解法，注意函数思想、数形结合思想的应用．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列{an}中，a1=t（t∈R，且t≠0，1），a2=t2，且当x=t时，f（x）=
    1
    2
    （an-an-1）x2-（an+1-an）x（n≥2）取得极值?
    （1）求证：数列{an+1-an}是等比数列；
    （2）若bn=anln|an|（n∈N*），求数列{bn}的前n项和Sn；
    （3）当t=-
    7
    10
    时，数列{bn}中是否存在最大项？如果存在，说明是第几项；如果不存在，请说明理由?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设定义在R上的函数f（x）满足对?x，t∈R，且t≠0，都有t（f（x+t）-f（x））＞0，则{（x，y）|y=f（x）}∩{（x，y）|y=a}的元素个数为
    0或1
    0或1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    t∈R，且t∈(0，10)，由t确定两个任意点P(t，t)，Q(10－t，0)．

    问：(1)直线PQ是否能通过下面的点M(6，1)，N(4，5)；

    (2)在△OPQ内作内接正方形ABCD，顶点A、B在边OQ上，顶点C在边PQ上，顶点D在边OP上．①求证：顶点C一定在直线上．

    ②求下图中阴影部分面积的最大值，并求这时顶点A、B、C、D的坐标．w.w.w.k.s.5.u.c.o.m       

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖北省武汉市高三第5次月考数学理卷 题型：解答题

    (本小题满分14分)

    已知数列{an}中，a1＝t(t∈R，且t≠0,1)，a2＝t2，且当x＝t时，

    函数f(x)＝(an－an－1)x2－(an＋1－an)x(n≥2，n∈N?)取得极值.

    (Ⅰ)求证：数列{an＋1－an}是等比数列；

    (Ⅱ)若bn＝anln|an|(n∈N?)，求数列{bn}的前n项和Sn；

    (Ⅲ)当t＝－时，数列{bn}中是否存在最大项？如果存在，说明是第几项；如果不存在，请说明理由.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2011年江苏省高考数学权威预测试卷（1）（解析版） 题型：解答题

    设定义在R上的函数f（x）满足对?x，t∈R，且t≠0，都有t（f（x+t）-f（x））＞0，则{（x，y）|y=f（x）}∩{（x，y）|y=a}的元素个数为    ．

    查看答案和解析>>

    同步练习册答案