
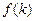 是满足不等式
是满足不等式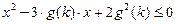 的自然数
的自然数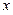 的个数,其中
的个数,其中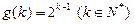 .
.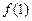 的值;
的值;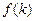 的解析式;
的解析式; ,令
,令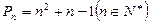 ,试比较
,试比较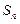 与
与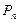 的大小.
的大小.
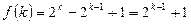
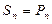 ;当n=3时,
;当n=3时,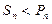 ;当n=1或
;当n=1或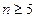 时
时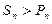 ;---14分
;---14分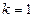
 时,原不等式即
时,原不等式即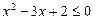 ,解得
,解得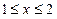 ,
,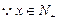 ∴
∴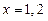 即
即 ------------------------------2分
------------------------------2分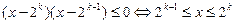 ……………………………………………..4分
……………………………………………..4分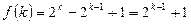 ………………………………………………………..6分
………………………………………………………..6分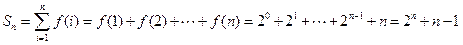 ……8分
……8分
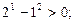 ;n=2时,
;n=2时,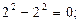
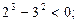 ;n=4时,
;n=4时,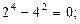
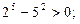 ;n=6时,
;n=6时,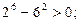 …………………………………………9分
…………………………………………9分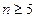 时
时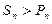 下面用数学归纳法给出证明
下面用数学归纳法给出证明 ,已证…………………………………………………….10分
,已证…………………………………………………….10分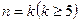 时结论成立即
时结论成立即

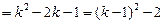
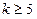 范围内,
范围内, 恒成立,则
恒成立,则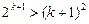 ,即
,即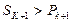
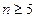 时,
时,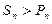 ………………………………….. 13分
………………………………….. 13分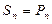 ;当n=3时,
;当n=3时,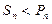 ;当n=1或
;当n=1或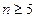 时
时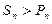 ;---14分
;---14分

科目:高中数学 来源:不详 题型:解答题
 为常数,且
为常数,且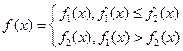 。
。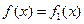 对所有的实数
对所有的实数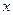 成立的充要条件(用
成立的充要条件(用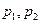 表示);
表示);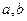 为两实数,
为两实数,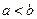 且
且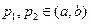 ,若
,若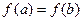 ,求证:
,求证: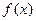 在区间
在区间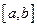 上的单调增区间的长度和为
上的单调增区间的长度和为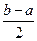 (闭区间
(闭区间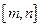 的长度定义为
的长度定义为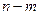 )。
)。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
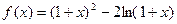
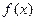 的单调增区间和单调减区间;
的单调增区间和单调减区间;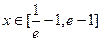 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式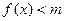 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;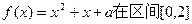 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
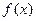 ,若存在闭区间
,若存在闭区间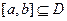 和常数
和常数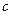 ,使得对任意
,使得对任意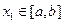 ,都有
,都有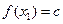 ,且对任意
,且对任意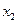 ∈D,当
∈D,当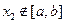 时,
时,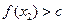 恒成立,则称函数
恒成立,则称函数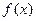 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.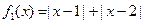 和
和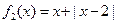 是否为R上的“平底型”函数? 并说明理由;
是否为R上的“平底型”函数? 并说明理由;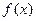 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式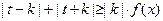 对一切
对一切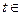 R恒成立,求实数
R恒成立,求实数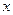 的取值范围;
的取值范围;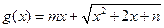 是区间
是区间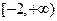 上的“平底型”函数,求
上的“平底型”函数,求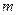 和
和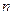 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
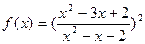 (其中
(其中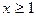 且
且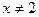 )
)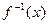
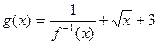 ,求函数g(x)最小值及相应的x值;
,求函数g(x)最小值及相应的x值;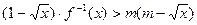 对于区间
对于区间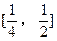 上的每一个x值都成立,求实数m的取值范围。
上的每一个x值都成立,求实数m的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
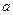 的
的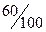 ,目前我国的减排手段有两种,第一种是通过引进新技术,新工艺使得每年的炭排放比上一年炭排放总量均减少
,目前我国的减排手段有两种,第一种是通过引进新技术,新工艺使得每年的炭排放比上一年炭排放总量均减少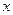 个百分点,第二种是通过教育与宣传使得全体国民具有节能减排的意识,进而减少炭排放。
个百分点,第二种是通过教育与宣传使得全体国民具有节能减排的意识,进而减少炭排放。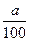 ,求2011年我国的炭排放量
,求2011年我国的炭排放量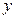 个百分点,要保证完成减排目标,求
个百分点,要保证完成减排目标,求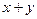 满足的范围。(已知
满足的范围。(已知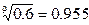 ,
,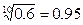 ,
,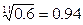 ,
,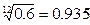 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com