
【题目】已知![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 时,
时,![]() 的值域:
的值域:
(3)设![]() ,若
,若![]() 对任意的
对任意的![]() ,总有
,总有![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时
时![]() 的值域为
的值域为![]() ;当
;当![]() 时
时![]() 的值域为
的值域为![]() ;(3)
;(3)![]() .
.
【解析】
(1)使用换元法令![]() 即可得解;
即可得解;
(2)令![]()
![]() ,则
,则![]() ,根据
,根据![]() 的取值结合一次函数、二次函数的性质即可得解.
的取值结合一次函数、二次函数的性质即可得解.
(3)转化条件为![]() .令
.令![]() 得
得![]() ,根据
,根据![]() 的范围讨论
的范围讨论![]() 时函数
时函数![]() 的最值即可得解.
的最值即可得解.
(1)设![]() ,则
,则![]() ,所以
,所以![]()
所以![]() ;
;
(2)设![]() ,
,![]() ,则
,则![]() ,
,
所以![]()
当![]() 时,
时,![]() ,
,![]() 的值域为
的值域为![]()
当![]() 时,
时,![]()
若![]() ,对称轴
,对称轴![]() ,
,![]() 的值域为
的值域为![]() ,
,
若![]() ,对称轴
,对称轴![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() 的值域为
的值域为![]() .
.
综上,当![]() 时
时![]() 的值域为
的值域为![]() ;当
;当![]() 时
时![]() 的值域为
的值域为![]() .
.
(3)化简得![]() ,
,
对任意![]() 总有
总有![]() ,
,
∴![]() 在
在![]() 满足
满足![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 即
即![]() 时
时![]() 在区间
在区间![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ,所以
,所以![]() ,则
,则![]()
当![]() 时,下证函数
时,下证函数![]() 在区间
在区间![]() 单调递增:
单调递增:
任取![]() ,
,
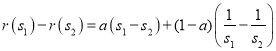
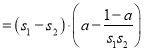 ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又 ![]() ∴
∴![]() 即函数
即函数![]() 在区间
在区间![]() 单调递增,
单调递增,
又 ![]() 时,
时,![]() 恒成立,∴
恒成立,∴![]() 满足要求.
满足要求.
综上![]() 的取值范围为
的取值范围为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,梯形![]() 是平面图形
是平面图形![]() 的直观图.其中
的直观图.其中![]() .
.
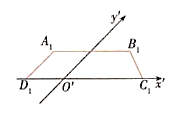
(1)如何利用斜二测画法的规则画出原四边形?
(2)在问题(1)中,如何求出水平放置的平面图形与直观图的面积?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
A. 3690 B. 3660 C. 1845 D. 1830
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两点![]() 满足条件:①
满足条件:①![]() 都在函数
都在函数![]() 的图象上;②
的图象上;②![]() 关于原点对称.则称点对
关于原点对称.则称点对![]() 是函数
是函数![]() 的一对“友好点对”(点对
的一对“友好点对”(点对![]() 与
与![]() 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数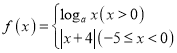 (
(![]() 且
且![]() ),若此函数的“友好点对”有且只有一对,则
),若此函数的“友好点对”有且只有一对,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
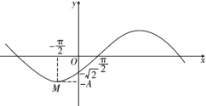
【题目】函数![]() 的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点的坐标为
的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点的坐标为![]() ,与y轴的交点坐标为
,与y轴的交点坐标为![]() .
.
(1)求A,![]() ,
,![]() 的值;
的值;
(2)若关于x的方程![]() 在
在![]() 上有一解,求实数m的取值范围.
上有一解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:

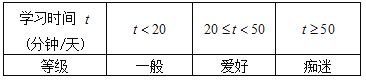
根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记![]() 为选出的两人中甲大学的人数,求
为选出的两人中甲大学的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值![]() 与
与![]() 的大小,及方差
的大小,及方差![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良后所排放的废气中含有的污染物数量为
,首次改良后所排放的废气中含有的污染物数量为![]() .设改良工艺前所排放的废气中含有的污染物数量为
.设改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良工艺后所排放的废气中含有的污染物数量为
,首次改良工艺后所排放的废气中含有的污染物数量为![]() ,则第n次改良后所排放的废气中的污染物数量
,则第n次改良后所排放的废气中的污染物数量![]() ,可由函数模型
,可由函数模型![]() 给出,其中n是指改良工艺的次数.
给出,其中n是指改良工艺的次数.
(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过![]() ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
(参考数据:取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(2)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,下个月分别在两个不同的网店进行销售,求这两个网店下个月获得奖励的总额![]() 的分布列及其数学期望.
的分布列及其数学期望.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为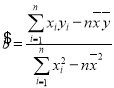 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com