某企业2012年初用72万元购进一台设备,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为50万元,设使用n后该设备的盈利额为f(n)
(Ⅰ)写出f(n)的表达式
(Ⅱ)求从第几年开始,该设备开始盈利;
(Ⅲ)用若干年后,对该设备的处理方案有两种:方案一:年平均盈利额达到最大值时,以48万元价格处理该设备;方案二:当盈利额达到最大值时,以16万元价格处理该设备.问用哪种方案处理较为合理?请说明理由.
【答案】
分析:(Ⅰ)由题意,根据第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,由此可得f(n)的表达式
(Ⅱ)由f(n)>0,即可得到结论;
(Ⅲ)方案①利用基本不等式求最值,方案②利用配方法求最值,比较即可得到结论.
解答:解:(Ⅰ)由题意得:f(n)=50n-72-[12n+

•4]=-2n
2+40n-72(n∈N
+).…(3分)
(Ⅱ)由f(n)>0得:-2n
2+40n-72>0即n
2-20n+36<0,解得2<n<8,
由n∈N
+知,从第三年开始盈利…(6分
(Ⅲ)方案①:年平均纯利润
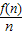
=40-2(n+
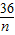
)≤16,当且仅当n=6时等号成立.
故方案①共获利6×16+48=144(万元),此时n=6.…(10分)
方案②:f(n)=-2(n-10)
2+128.当n=10时,f(n)
max=128.
故方案②共获利128+16=144(万元).…(13分)
比较两种方案,获利都是144万元,但由于第①种方案只需6年,而第②种方案需10年,故选择第①种方案更合算.…(14分)
点评:本题考查函数模型的构建,考查利用基本不等式与配方法求函数的最值,属于中档题.

 •4]=-2n2+40n-72(n∈N+).…(3分)
•4]=-2n2+40n-72(n∈N+).…(3分)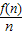 =40-2(n+
=40-2(n+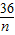 )≤16,当且仅当n=6时等号成立.
)≤16,当且仅当n=6时等号成立.
