
【题目】己知函数![]()
(1)当![]() 时,设函数
时,设函数![]() ,求函数
,求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)设![]() 是
是![]() 的导函数,若
的导函数,若![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,当
,当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)当![]() ,
,![]() 单调递减;
单调递减; ![]()
![]() 单调递增, 当
单调递增, 当![]() ,取得极小值
,取得极小值![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() 的最大值
的最大值![]() ,
,![]() 的最小值
的最小值![]() .
.
【解析】
(1)把![]() 代入
代入![]() 可得
可得![]() ,对
,对![]() 求导可得其单调区间和极值;
求导可得其单调区间和极值;
(2)对![]() 求导可得
求导可得![]() 在
在![]() 恒成立,设
恒成立,设![]() ,对
,对![]() 求导,可得
求导,可得![]() 有最小值,可得
有最小值,可得![]() 的取值范围;
的取值范围;
(3)对![]() 求导,可得当
求导,可得当![]() ,
,![]() 单调递增,当
单调递增,当![]() ,
,![]() 单调递减,可得可得
单调递减,可得可得![]() 的最大值,设
的最大值,设![]() ,对
,对![]() 求导,可得
求导,可得![]() 的最小值.
的最小值.
解:(1)当![]() 时,
时,![]() ,可得
,可得![]() ,
,
令![]() ,可得
,可得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() ,
,![]() 单调递增;
单调递增;
可得当![]() ,取得极小值
,取得极小值![]() ;
;
(2)![]() ,
,![]() ,
,
即![]() ,
,![]() 在
在![]() 恒成立,
恒成立,
设![]() ,可得
,可得![]() ,
,
令![]() ,可得
,可得![]() ,
,
当![]() ,
,![]() ,函数单调递减,
,函数单调递减,
当![]() ,
,![]() ,函数单调递增,
,函数单调递增,
当![]() 有最小值,可得
有最小值,可得![]() ,
,
![]() ,
,![]() ;
;
(3)由![]() ,可得
,可得![]() ,
,
当![]() ,可得
,可得![]() ,
,
所以![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,
所以![]() ,
,![]() 单调递减;
单调递减;
可得![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
又![]() ,可得
,可得![]() 的最大值
的最大值![]()
设![]()
其中![]() ,可得
,可得![]() ,
,
故![]() 在
在![]() 单调递增,可得
单调递增,可得![]() ,即
,即![]() ,
,
故可得![]() 的最小值
的最小值![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率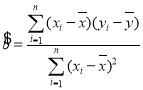 ;相关系数
;相关系数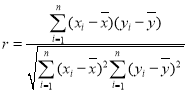 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
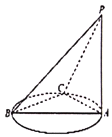
【题目】如图,![]() 垂直于以
垂直于以![]() 为直径的圆所在的平面,点
为直径的圆所在的平面,点![]() 是圆周上异于
是圆周上异于![]() ,
,![]() 的任意一点,则下列结论中正确的是( )
的任意一点,则下列结论中正确的是( )
①![]()
②![]()
③![]() 平面
平面![]()
④平面![]() 平面
平面![]()
⑤平面![]() 平面
平面![]()
A.①②⑤B.②⑤C.②④⑤D.②③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
![]() 如果随机调查这个班的一名学生,求事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率;
如果随机调查这个班的一名学生,求事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率;
![]() 若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,请用字母代表不同的学生列举出抽取的所有可能结果;
若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,请用字母代表不同的学生列举出抽取的所有可能结果;
![]() 在
在![]() 的条件下,求事件B:两名学生中恰有1名男生的概率.
的条件下,求事件B:两名学生中恰有1名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学学生参加数学竞赛培训,在培训期间他们参加5项预赛,成绩如下:
甲:78 76 74 90 82
乙:90 70 75 85 80
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从平均数、方差的角度考虑,你认为选派哪位学生参加合适?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下结论正确的个数是( )
①若数列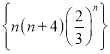 中的最大项是第
中的最大项是第![]() 项,则
项,则![]() .
.
②在![]() 中,若
中,若![]() ,则
,则![]() 为等腰直角三角形.
为等腰直角三角形.
③设![]() 、
、![]() 分别为等差数列
分别为等差数列![]() 与
与![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() .
.
④![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,若
,若![]() 、
、![]() 、
、![]() 成等比数列,且
成等比数列,且![]() ,则
,则![]() .
.
⑤在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 所对边,
所对边,![]() ,则
,则![]() 的取值范围为
的取值范围为![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com