练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列函数在区间（﹣∞，0）上是增函数的是（ ）
    A.f（x）=x2﹣4x
    B.g（x）=3x+1
    C.h（x）=3﹣x
    D.t（x）=tanx

    【答案】B
    【解析】解：对于A，f（x）=x2﹣4x=（x﹣2）2﹣4，在（﹣∞，0）上是单调减函数，不满足题意；

    对于B，g（x）=3x+1在（﹣∞，0）上是单调增函数，满足题意；

    对于C，h（x）=3﹣x= 是（﹣∞，0）上的单调减函数，不满足题意；

    对于D，t（x）=tanx在区间（﹣∞，0）上是周期函数，不是单调函数，不满足题意．

    B故选：B．

    【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列命题： ①平面A′FG⊥平面ABC；
    ②BC∥平面A′DE；
    ③三棱锥A′﹣DEF的体积最大值为 a3；
    ④动点A′在平面ABC上的射影在线段AF上；
    ⑤二面角A′﹣DE﹣F大小的范围是[0， ]．
    其中正确的命题是（写出所有正确命题的编号）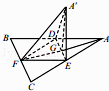

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，∠ACB=90°．BC=CC1=a，AC=2a．
    （1）求证：AB1⊥BC1；
    （2）求二面角B﹣AB1﹣C的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面是被严重破坏的频率分布表和频率分布直方图，根据残表和残图，则 p= ， q= ．

    分数段

    频数

    [60，70）

    p

    [70，80）

    90

    [80，90）

    60

    [90，100]

    20

    q

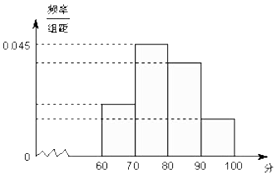
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 ， ， 是同一平面内的三个向量，其中 =（﹣ ，1）．
    （1）若| |=2 且 ∥ ，求 的坐标；
    （2）若| |= ，（ +3 ）⊥（ ﹣ ），求向量 ， 的夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和Sn=3n2+8n，{bn}是等差数列，且an=bn+bn+1 ． （Ⅰ）求数列{bn}的通项公式；
    （Ⅱ）令cn= ，求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD﹣A1B1C1D1的棱线长为1，线段B1D1上有两个动点E，F，且EF= ，则下列结论中错误的是（ ）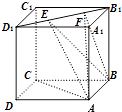
    A.AC⊥BE
    B.EF∥平面ABCD
    C.三棱锥A﹣BEF的体积为定值
    D.异面直线AE，BF所成的角为定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）判断f（x）的奇偶性；
    （2）用单调性的定义证明f（x）为R上的增函数；
    （3）若对任意的t∈R，不等式f（mt2+1）+f（1﹣mt）＞0恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|2x﹣6≤2﹣2x≤1}，B={x|x∈A∩N}，C={x|a≤x≤a+1}． （Ⅰ）写出集合B的所有子集；
    （Ⅱ）若A∩C=C，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案