
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | |a|<|b| | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ${(\frac{1}{2})^a}>{(\frac{1}{2})^b}$ | D. | lna>lnb |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
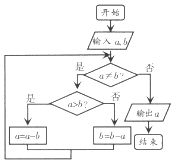 右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别为16,24,则输出的a的值为( )
右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别为16,24,则输出的a的值为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“$?{x_0}∈R,{x_0}^2+1>3{x_0}$”的否定是“$?{x_0}∈R,{x^2}+1>3x$” | |
| B. | “函数f(x)=cosax-sinax的最小正周期为 π”是“a=2”的必要不充分条件 | |
| C. | x2+2x≥ax在x∈[1,2]时有解?(x2+2x)min≥(ax)min在x∈[1,2]时成立 | |
| D. | “平面向量$\overrightarrow a$与$\overrightarrow b$的夹角是钝角”的充分必要条件是“$\overrightarrow a$•$\overrightarrow b$<0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com