
分析 (1)由椭圆的定义可知:△ABF2的周长=丨AB丨+丨AF2丨+丨BF2丨=4a=8,则△ABF2的周长8;
(2)由(1)可知:直线AB的方程为y=x+1,代入椭圆方程,由韦达定理及弦长公式即可求得弦长|AB|.
解答 解 (1)椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,a=2,b=$\sqrt{3}$,c=1,
由椭圆的定义,得丨AF1丨+丨AF2丨=2a=4,丨BF1丨+丨BF2丨=2a=4,
又丨AF1丨+丨BF1丨=丨AB丨,
∴△ABF2的周长=丨AB丨+丨AF2丨+丨BF2丨=4a=8.
∴故△ABF2点周长为8;
(2)由(1)可知,得F1(-1,0),
∵AB的倾斜角为$\frac{π}{4}$,则AB斜率为1,A(x1,y1),B(x2,y2),
故直线AB的方程为y=x+1.$\left\{\begin{array}{l}{y=x+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:7y2-6y-9=0,
由韦达定理可知:y1+y2=$\frac{6}{7}$,y1•y2=-$\frac{9}{7}$,
则由弦长公式丨AB丨=$\sqrt{1+\frac{1}{{k}^{2}}}$•$\sqrt{({y}_{1}+{y}_{2})-4{y}_{1}{y}_{2}}$=$\sqrt{1+1}$•$\sqrt{(\frac{6}{7})^{2}-4×(-\frac{9}{7})}$=$\frac{24}{7}$,
弦长|AB|=$\frac{24}{7}$.
点评 本题考查椭圆的定义,直线与椭圆的位置关系,考查韦达定理,弦长公式,考查计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
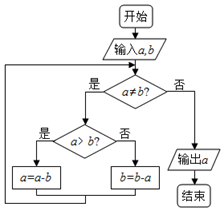 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )| A. | 9 | B. | 3 | C. | 7 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com