
【题目】
周销售量(单位:吨) | 2 | 3 | 4 |
频数 | 20 | 50 | 30 |
⑴ 根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵ 已知每吨该商品的销售利润为2千元,![]() 表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】⑴周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3
⑵分布列见解析,12.4(千元)
【解析】本小题主要考查频率、概率等基础知识,考查运用概率知识解决实际问题的能力.考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件.
(1)由题意得到样本容量是100,周销售量为2吨,3吨和4吨的频数分别为20、50、30,利用样本容量、频数和频率之间的关系得到周销售量分别为2吨,3吨和4吨的频率分别为0.2,0.5和0.3.
(2)由题意知本题是一个独立重复试验,根据对立事件和独立重复试验的公式得到要求的结论,实际上本题的关键是理解题意,看清题目的本质,利用数学知识解决实际问题.
解:(1)周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3. ……3分
(2)![]() 的可能值为8,10,12,14,16, ……4分
的可能值为8,10,12,14,16, ……4分
P(![]() =8)=0.22=0.04, P(
=8)=0.22=0.04, P(![]() =10)=2×0.2×0.5=0.2, ……6分
=10)=2×0.2×0.5=0.2, ……6分
P(![]() =12)=0.52+2×0.2×0.3=0.37, P(
=12)=0.52+2×0.2×0.3=0.37, P(![]() =14)=2×0.5×0.3=0.3,
=14)=2×0.5×0.3=0.3,
P(![]() =16)=0.32=0.09. ……9分
=16)=0.32=0.09. ……9分
则![]() 的分布列为
的分布列为
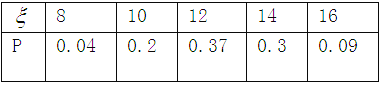 ……10分
……10分![]() =8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元) ……12分
=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元) ……12分


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]()
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上有且只有一个极值点,求实数
在定义域上有且只有一个极值点,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
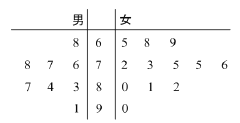
【题目】某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示.成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
(Ⅰ)求出8名男生的平均成绩和12 名女生成绩的中位数;
(Ⅱ)按照获奖类型,用分层抽样的方法从这20名学生中抽取5人,再从选出的5人中任选3人,求恰有1人获“优秀奖”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲参加A,B,C三个科目的学业水平考试,其考试成绩合格的概率如下表,假设三个科目的考试甲是否成绩合格相互独立.
科目A | 科目B | 科目C | |
甲 |
|
|
|
(I)求甲至少有一个科目考试成绩合格的概率;
(Ⅱ)设甲参加考试成绩合格的科目数量为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 为坐标原点,动点
为坐标原点,动点![]() 满足:
满足:![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 都过点
都过点![]() ,且
,且![]() ,
,![]() 与轨迹
与轨迹![]() 分别交于点
分别交于点![]() ,试探究是否存在这样的直线?使得
,试探究是否存在这样的直线?使得![]() 是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某综艺节目为增强娱乐性,要求现场嘉宾与其场外好友连线互动.凡是拒绝表演节目的好友均无连线好友的机会;凡是选择表演节目的好友均需连线未参加过此活动的![]() 个好友参与此活动,以此下去.
个好友参与此活动,以此下去.
(Ⅰ)假设每个人选择表演与否是等可能的,且互不影响,则某人选择表演后,其连线的![]() 个好友中不少于
个好友中不少于![]() 个好友选择表演节目的概率是多少?
个好友选择表演节目的概率是多少?
(Ⅱ)为调查“选择表演者”与其性别是否有关,采取随机抽样得到如下列表:
选择表演 | 拒绝表演 | 合计 | |
男 | 50 | 10 | 60 |
女 | 10 | 10 | 20 |
合计 | 60 | 20 | 80 |
①根据表中数据,是否有![]() 的把握认为“表演节目”与好友的性别有关?
的把握认为“表演节目”与好友的性别有关?
②将此样本的频率视为总体的概率,随机调查![]() 名男性好友,设
名男性好友,设![]() 为
为![]() 个人中选择表演的人数,求
个人中选择表演的人数,求![]() 的分布列和期望.
的分布列和期望.
附:![]() ;
;
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在![]() 天每件的销售价格
天每件的销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (天)之间的关系如下表:
(天)之间的关系如下表:
|
|
|
|
|
|
|
|
|
|

(![]() )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(![]() )根据表
)根据表![]() 提供的数据,写出日销售量
提供的数据,写出日销售量![]() 与时间
与时间![]() 的一次函数关系式.
的一次函数关系式.
(![]() )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是![]() 天中的第几天.(日销售金额
天中的第几天.(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2014课标全国Ⅰ,文12】已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin ωx·cos ωx+![]() cos2ωx-
cos2ωx-![]()
(ω>0),直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为![]() .
.
(Ⅰ)求f(x)的表达式;
(Ⅱ)将函数f(x)的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的单调减区间.
个单位长度后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com