
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①当![]() 时,有
时,有![]() ;
;
②若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
③已知![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() ;
;
④函数![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
⑤当![]() 时,不等式
时,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为
的取值范围为![]() .
.
其中正确命题的序号为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y2=2x与C2:y=![]() x2在第一象限内的交点为P.
x2在第一象限内的交点为P.
(1)求过点P且与曲线C2相切的直线方程;
(2)求两条曲线所围图形(如图所示的阴影部分)的面积S.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇环形ABCD,作圆台容器的侧面,并且在余下的扇形OCD内能剪下一块与其相切的圆形使它恰好作圆台容器的下底面(大底面).试求:
(1)AD应取多长?
(2)容器的容积为多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点.
(1)求圆A的方程;
(2)当|MN|=2时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2008奥运会上两名射击运动员甲、乙在比赛中打出如下成绩:甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩如图所示,茎表示成绩的整数环数,叶表示小数点后的数字.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
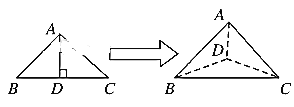
①BD⊥AC; ②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC。
其中正确的是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求三棱锥E—ABC的体积V.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com