
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线C相交于A,B两点,与圆
与抛物线C相交于A,B两点,与圆![]() 相交于D,E两点,O为坐标原点,
相交于D,E两点,O为坐标原点,![]() ,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
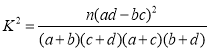 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是
旋转过程中的一个图形,下列命题中,错误的是

A. 恒有![]() ⊥
⊥![]()
B. 异面直线![]() 与
与![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 先把高二年级的2000名学生编号为1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() 的学生,这样的抽样方法是系统抽样法;
的学生,这样的抽样方法是系统抽样法;
B. 独立性检验中,![]() 越大,则越有把握说两个变量有关;
越大,则越有把握说两个变量有关;
C. 若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1;
的值越接近于1;
D. 若一组数据1、a、3的平均数是2,则该组数据的方差是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人射击,已知甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() .
.
(1)两人各射击一次,求至少有一人击中目标的概率;
(2)若制定规则如下:两人轮流射击,每人至多射击2次,甲先射,若有人击中目标即停止射击.
①求乙射击次数不超过1次的概率;
②记甲、乙两人射击次数和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个正多边形的每条边和对角线恰各染成2018种颜色之一,且所有边及对角线不全同色.若正多边形中不存在两色三角形(即三角形的三边恰被染成两种颜色),则称该多边形的染色是“和谐的”.求最大的正整数![]() ,使得存在一个和谐的染色正
,使得存在一个和谐的染色正![]() 边形.
边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com