
【题目】在以下关于向量的命题中,不正确的是( )
A.若向量 ![]() ,向量
,向量 ![]() (xy≠0),则
(xy≠0),则 ![]()
B.若四边形ABCD为菱形,则 ![]()
C.点G是△ABC的重心,则 ![]()
D.△ABC中, ![]() 和
和 ![]() 的夹角等于A
的夹角等于A
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an},{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1,设p:函数y=loga(x+1)在(0,+∞)上单调递减;q:曲线y=x2+(2a﹣3)x+1与x轴交于不同的两点.如果p且q为假命题,p或q为真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,如果![]() 与
与![]() 都是整数,就称点
都是整数,就称点![]() 为整点,下列命题中正确的是__________.(写出所有正确命题的编号)
为整点,下列命题中正确的是__________.(写出所有正确命题的编号)
①存在这样的直线,既不与坐标轴平行又不经过任何整点;
②若![]() 与
与![]() 都是无理数,则直线
都是无理数,则直线![]() 不经过任何整点;
不经过任何整点;
③直线![]() 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当![]() 经过两个不同的整点;
经过两个不同的整点;
④直线![]() 经过无穷多个整点的充分必要条件是:
经过无穷多个整点的充分必要条件是: ![]() 与
与![]() 都是有理数;
都是有理数;
⑤存在恰经过一个整点的直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三次函数的导函数![]() ,
, ![]() ,
, ![]() 为实数.
为实数.
(1)若曲线![]() 在点
在点![]() 处切线的斜率为12,求
处切线的斜率为12,求![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上的最小值,最大值分别为
上的最小值,最大值分别为![]() ,1,且
,1,且![]() ,求函数
,求函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在点
在点![]() 处切线方程为y=3x+b,求a,b的值;
处切线方程为y=3x+b,求a,b的值;
(Ⅱ)当a>0时,求函数![]() 在[1,2]上的最小值;
在[1,2]上的最小值;
(Ⅲ)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得
,使得![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题: (Ⅰ) 求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 设学生甲、乙的成绩属于区间[40,50),现从成绩属于该区间的学生中任选两人,求甲、乙中至少有一人被选的概率.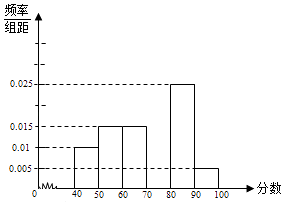
查看答案和解析>>
科目:高中数学 来源: 题型:
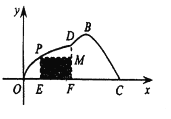
【题目】如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路![]() ,另一侧修建一条休闲大道,它的前一段
,另一侧修建一条休闲大道,它的前一段![]() 是函数
是函数![]() ,
, ![]() 的一部分,后一段
的一部分,后一段![]() 是函数
是函数![]() (
(![]() ,
, ![]() ),
),![]() 时的图象,图象的最高点为
时的图象,图象的最高点为![]() ,
, ![]() ,垂足为
,垂足为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点![]() 落在曲线
落在曲线![]() 上何处时,儿童乐园的面积最大?
上何处时,儿童乐园的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com