
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,0)∪(0,1) |
分析 若$\overrightarrow a$与$\overrightarrow a$+λ$\overrightarrow b$夹角为锐角,则其数量积大于0,还需要保证λ≠0,问题得以解决.
解答 解:∵$\overrightarrow a$=(1,-2),$\overrightarrow b$=(3,4),$\overrightarrow a$与$\overrightarrow a$+λ$\overrightarrow b$夹角为锐角,
∴$\overrightarrow a$•($\overrightarrow a$+λ$\overrightarrow b$)>0,
∴$\overrightarrow a$2+λ$\overrightarrow a$•$\overrightarrow b$>0,
即5+λ(1×3-2×4)>0,
解得λ<1,
又λ=0时,$\overrightarrow a$与$\overrightarrow a$+λ$\overrightarrow b$夹角为0°,
综上所述实数λ的取值范围是(-∞,0)∪(0,1),
故选:D.
点评 本题考查数量积表示两个向量的夹角,考查计算能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4项 | B. | 5项 | C. | 6项 | D. | 7项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{3}$个单位 | B. | 向左平行移动$\frac{π}{9}$个单位 | ||
| C. | 向右平行移动$\frac{π}{3}$个单位 | D. | 向右平行移动$\frac{π}{9}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
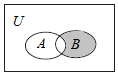
| A. | {3} | B. | {2,4} | C. | {2,3,4} | D. | {3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com