练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，以为极点， 轴正半轴为极轴建立极坐标系，曲线的极坐标方程为， 是曲线与直线： （）的交点（异于原点）．

    （1）写出， 的直角坐标方程；

    （2）求过点和直线垂直的直线的极坐标方程．

    【答案】（1）曲线的直角坐标方程为．曲线： （）的直角坐标方程为.（2）.

    【解析】试题分析：（1）利用，即可得的直角坐标方程，由直线： ，故原点，知斜率为1，进而得方程；

    （2）联立解得或，由垂直得直线的斜率为-1，进而得直角坐标方程，换为极坐标方程即可.

    试题解析：（1）由，得，则．

    即，

    即曲线的直角坐标方程为．

    曲线： （）的直角坐标方程为．

    （2）联立解得或

    故点的坐标为，

    所以过点和直线垂直的直线的直角坐标方程为，即，

    化为极坐标方程是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)= ,若f(x)的图象与直线y=kx有两个不同的交点，则实数k的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， .

    （1）求函数的单调区间；

    （2）若函数在处取得极大值，求正实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象与轴相切，且切点在轴的正半轴上.

    （1）求曲线与轴，直线及轴围成图形的面积；

    （2）若函数在上的极小值不大于，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

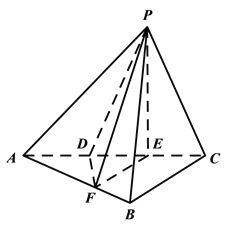
    【题目】如图，三棱锥P-ABC中，平面PAC平面ABC， ABC=，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF//BC.

    (Ⅰ)证明：AB平面PFE.

    (Ⅱ)若四棱锥P-DFBC的体积为7，求线段BC的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（sinx+cosx）2-2cos2x，

    （1）求函数f（x）的最小正周期和单调递减区间；

    （2）当x∈时，求f（x）的最大值和最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:

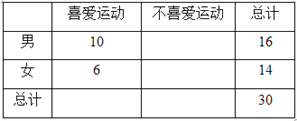
    (1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.

    (2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数的分布列及数学期望.

    参考公式: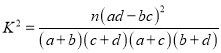

    参考数据:

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知下列命题：

    ①命题“， ”的否定是：“， ”；

    ②若样本数据的平均值和方差分别为和则数据的平均值和标准差分别为， ；

    ③两个事件不是互斥事件的必要不充分条件是两个事件不是对立事件；

    ④在列联表中，若比值与相差越大，则两个分类变量有关系的可能性就越大．

    ⑤已知为两个平面，且， 为直线．则命题:“若，则”的逆命题和否命题均为假命题．

    ⑥设定点、，动点满足条件为正常数），则的轨迹是椭圆．其中真命题的个数为( )

    A. 5 B. 4 C. 3 D. 2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某公司生产某产品的年固定成本为100万元，每生产1千件需另投入27万元，设该公司一年内生产该产品千件并全部销售完，每千件的销售收入为万元，且.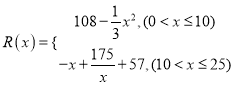

    ⑴ 写出年利润（万元）关于年产量（千件）的函数解析式；

    ⑵ 当年产量为多少千件时，该公司在这一产品的生产中所获年利润最大？（注：年利润＝年销售收入年总成本）.

    查看答案和解析>>

    同步练习册答案