
分析 可设f(x)=2x,g(x)=x2,容易得到f(2)=g(2),f(4)=g(4),f(x)在x=4之后增长速度大于g(x)的增长速度,可画出这两函数的图象,便可看出这两函数有两个交点,从而便可得出A∩B.
解答  解:函数y=2x在R上单调递增,y=x2在(0,+∞)上单调递增;
解:函数y=2x在R上单调递增,y=x2在(0,+∞)上单调递增;
根据这两个函数的图象可以看出,在x>4上y=2x的增长速度大于y=x2的增长速度,且两函数的有两个交点(2,4),(4,16),图象如下:
∴A∩B={(2,4),(4,16)};
故答案为:{(2,4),(4,16)}.
点评 考查描述法表示集合,点(x,y)作为元素,函数交点坐标和集合交集的关系,以及指数函数和二次函数的增长速度的对比.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:解答题
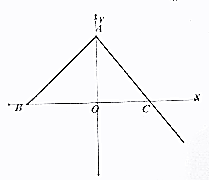 已知在平面直角坐标系中,O为坐标原点,A(0,4)、B(-4,0),点C是x轴正半轴上的点,△ABC的面积是14,O到AC的距离是$\frac{12}{5}$,动点P从A出发以每秒3个单位长度的速度沿射线AC运动,同时动点Q从C点出发以每秒2个单位的速度沿x轴的正方向运动.
已知在平面直角坐标系中,O为坐标原点,A(0,4)、B(-4,0),点C是x轴正半轴上的点,△ABC的面积是14,O到AC的距离是$\frac{12}{5}$,动点P从A出发以每秒3个单位长度的速度沿射线AC运动,同时动点Q从C点出发以每秒2个单位的速度沿x轴的正方向运动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 91 | B. | 90 | C. | 55 | D. | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com