
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为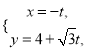 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线
分别交直线![]() 和曲线
和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应
的最大值及相应![]() 的值.
的值.
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】《聪明花开——莆仙话挑战赛》栏目共有五个项目,分别为“和一斗”“斗麻利”“文儒生”“放独步”“正功夫”.《聪明花开》栏目组为了解观众对项目的看法,设计了“你最喜欢的项目是哪一个”的调查问卷(每人只能选一个项目),对现场观众进行随机抽样调查,得到如下数据(单位:人):
和一斗 | 斗麻利 | 文儒生 | 放独步 | 正功夫 |
115 | 230 | 115 | 345 | 460 |
(1)在所有参与该问卷调查的人中,用分层抽样的方法抽取n人座谈,其中恰有4人最喜欢“斗麻利”,求n的值及所抽取的人中最喜欢“和一斗”的人数;
(2)在(1)中抽取的最喜欢“和一斗”和“斗麻利”的人中,任选2人参加栏目组互动,求恰有1人最喜欢“和一斗”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上的动点,直线
上的动点,直线![]() 的方程为
的方程为![]() .
.
①设直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
, ![]() ,求
,求![]() 的取值范围;
的取值范围;
②求与动直线![]() 恒相切的定椭圆
恒相切的定椭圆![]() 的方程;并探究:若
的方程;并探究:若![]() 是曲线
是曲线![]() :
: ![]() 上的动点,是否存在直线
上的动点,是否存在直线![]() :
: ![]() 恒相切的定曲线
恒相切的定曲线![]() ?若存在,直接写出曲线
?若存在,直接写出曲线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
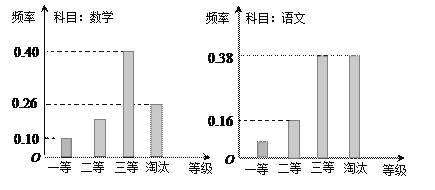

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 是公差为2的等差数列,数列
是公差为2的等差数列,数列![]() 满足b1=1,b2=2,且anbn+bn=nbn+1.
满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]()
对一切n∈N*恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)函数![]() 在
在![]() 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com