(本小题满分10分)已知函数
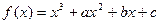
的图象过原点,且
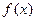
在
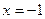
、
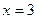
处取得极值.
(Ⅰ)求函数
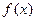
的单调区间及极值;
(Ⅱ)若函数
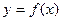
与
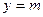
的图象有且仅有一个公共点,求实数
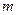
的取值范围.
(1)略(2)
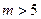
或
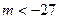
(I)
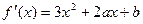
…………………………………1分
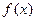
在
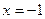
、
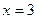
处取得极值,即
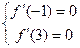
,
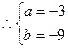
…………………3分
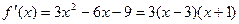
列表
…………………………………5分
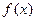
在
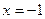
处取得极大值
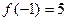
…………………………………6分
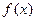
在
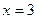
处取得极小值
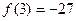
…………………………………7分
(II)
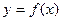
与
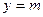
的图像有且仅有一个人公共点,
则极大值
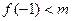
或极小值
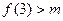
,即
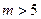
或
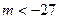
………………………10分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
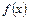
的导函数
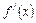
满足
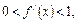
常数
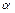
为方程
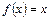
的实数根
(1)若函数
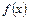
的定义域为I,对任意
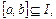
存在
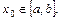
使等式
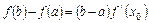
成立。 求证:方程
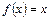
不存在异于
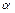
的实数根。
(2)求证:当
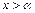
时,总有
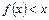
成立。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
设函数
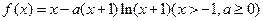
.
(Ⅰ)求
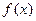
的单调区间;
(Ⅱ)当
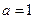
时,若方程
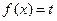
在
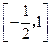
上有两个实数解,求实数
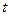
的取值范围;
(Ⅲ)求证:当
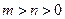
时,
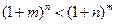
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分13分)
已知函数
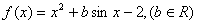
,且对任意
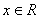
,有
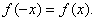
(1)求
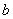
。
(2)已知
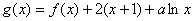
在区间(0,1)上为单调函数,求实数
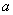
的取值范围。
(3)讨论函数
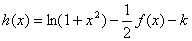
的零点个数?
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(满分14分)已知函数
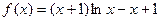
.
(1)若
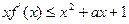
,求a的取值范围;
(2)证明:
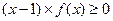
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
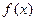
满足:
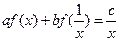
(其中
a、
b、
c均为常数,且|
a|≠|
b|),试求
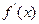
.
查看答案和解析>>

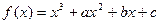 的图象过原点,且
的图象过原点,且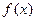 在
在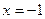 、
、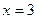 处取得极值.
处取得极值.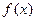 的单调区间及极值;
的单调区间及极值;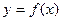 与
与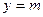 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数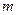 的取值范围.
的取值范围. 阅读快车系列答案
阅读快车系列答案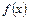 的导函数
的导函数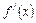 满足
满足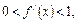 常数
常数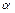 为方程
为方程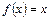
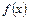 的定义域为I,对任意
的定义域为I,对任意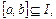 存在
存在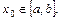 使等式
使等式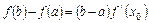 成立。 求证:方程
成立。 求证:方程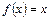 不存在异于
不存在异于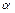 的实数根。
的实数根。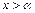 时,总有
时,总有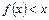 成立。
成立。