
【题目】已知圆![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,则直线
轴的正半轴,建立平面直角坐标系,则直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求圆![]() 的直角坐标方程,并求出圆心坐标和半径;
的直角坐标方程,并求出圆心坐标和半径;
(2)求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在
猜想”,是德国数学家洛萨克拉茨在![]() 年世界数学家大会上公布的一个猜想:任给一个正整数
年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘
为奇数就将它乘![]() 加
加![]() ,不断重复这样的运算,经过有限步后,最终都能够得到
,不断重复这样的运算,经过有限步后,最终都能够得到![]() ,得到
,得到![]() 即终止运算,己知正整数
即终止运算,己知正整数![]() 经过
经过![]() 次运算后得到
次运算后得到![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是中国最古老的天文学和数学著作,书中提到:从冬至之日起,小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影子长依次成等差数列,若冬至、立春、春分的日影子长的和是37.5尺,芒种的日影子长为4.5尺,则立夏的日影子长为:( )
A.15.5尺B.12.5尺C.9.5尺D.6.5尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解疫情期间哈一中高三学生的心理需求,更好的开展高考前的心理健康教育工作,心理老师设计了两个问题,第一个问题是“你出生的月份是奇数吗?”;第二个问题是“你是否需要心理疏导?”.让被调查者在保密的情况下掷一个均匀的骰子,其他人不知道掷骰子的结果,要求:当出现1点或2点时,回答第一个问题;否则回答第二个问题,由于其他人不知道他回答的是哪一个问题,因此,当他回答“是”时,你也无法知道他是否有心理问题,这种调查既保护了他的隐私,也能反映真实情况,可以从调查结果中得到需要的估计,若调查的900名学生中有156人回答“是”,由此可估计我校高三需要心理疏导的学生所占的比例约为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三十二班同学设计了一个如图所示的“蝴蝶形图案”(阴影区域)来预示在6月的高考中,同学们展翅高飞,其中![]() 是过抛物线
是过抛物线![]() 的焦点
的焦点![]() 的两条弦,且
的两条弦,且![]() ,点
,点![]() 为
为![]() 轴上一点,记
轴上一点,记![]() ,其中
,其中![]() 为锐角.
为锐角.
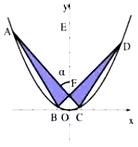
(1)求抛物线的方程;
(2)当“蝴蝶形图案”的面积最小时,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,P为直线
中,P为直线![]() :
:![]() 上的动点,动点Q满足
上的动点,动点Q满足![]() ,且原点O在以
,且原点O在以![]() 为直径的圆上.记动点Q的轨迹为曲线C
为直径的圆上.记动点Q的轨迹为曲线C
(1)求曲线C的方程:
(2)过点![]() 的直线
的直线![]() 与曲线C交于A,B两点,点D(异于A,B)在C上,直线
与曲线C交于A,B两点,点D(异于A,B)在C上,直线![]() ,
,![]() 分别与x轴交于点M,N,且
分别与x轴交于点M,N,且![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com