
【题目】设二次函数y=f(x)的最小值为4,且f(0)=f(2)=6,求f(x)的解析式.
【答案】解:∵二次函数y=f(x)满足f(0)=f(2),
∴二次函数y=f(x)图象的对称轴为 ![]() .
.
又∵二次函数y=f(x)的最小值为4,
∴二次函数y=f(x)图象的顶点坐标为(1,4),开口向上.
∴可设二次函数y=f(x)的解析式为f(x)=a(x﹣1)2+4(a>0).
∵f(0)=6,
∴a=2.
∴f(x)的解析式为f(x)=2x2﹣4x+6
【解析】本题可以根据条件找出抛物线的顶点,利用顶点式设出二次函数的解析式,再用一个点坐标代入,得到二次函数的解析式.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减).
上递减).


科目:高中数学 来源: 题型:
【题目】已知点(x,y)是区域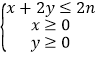 , (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
, (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
证明:数列{an﹣2}为等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的各项均为正数,且Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,S2=
,S2= ![]() ,S3=
,S3= ![]() .设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
.设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
(1)试求数列{an}的通项;
(2)求T=[log21]+[log22]+[log23]+…+[log2( ![]() ﹣1)]+[log2(
﹣1)]+[log2( ![]() )]关于n的表达式.
)]关于n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A=[0,![]() ),B=[
),B=[![]() , 1],函数f (x)=
, 1],函数f (x)= , 若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
, 若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
A.(0,![]() ]
]
B.[![]() ,
, ![]() ]
]
C.(![]() ,
, ![]() )
)
D.[0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的参数方程为 (θ是参数),直线l的极坐标方程为
(θ是参数),直线l的极坐标方程为![]() (ρ∈R)
(ρ∈R)
(Ⅰ)求C的普通方程与极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x 满足![]() ;
;
(1)若a=1且p∧q为真,求实数x的取值范围;
(2)若q是p的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax2﹣2ax+b(a≠0)在闭区间[1,2]上有最大值0,最小值﹣1,则a,b的值为( )
A.a=1,b=0
B.a=﹣1,b=﹣1
C.a=1,b=0或a=﹣1,b=﹣1
D.以上答案均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工科院校对![]() ,
, ![]() 两个专业的男女生人数进行调查,得到如下的列联表:
两个专业的男女生人数进行调查,得到如下的列联表:
专业 | 专业 | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(Ⅰ)从![]() 专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(Ⅱ)能否有95%的把握认为工科院校中“性别”与“专业”有关系?
附: 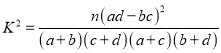 .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com