
分析 由题意可得直线l经过定点A(3,1).要使直线l被圆C截得的弦长最短,需CA和直线l垂直,利用勾股定理可得结论.
解答 解:圆C:(x-1)2+(y-2)2=25的圆心C(1,2)、半径为5,
直线l:(2m+1)x+(m+1)y-7m-4=0,即 m(2x+y-7)+(x+y-4)=0,
由$\left\{\begin{array}{l}{2x+y-7=0}\\{x+y-4=0}\end{array}\right.$,求得x=3,y=1,故直线l经过定点A(3,1).
要使直线l被圆C截得的弦长最短,需CA和直线l垂直,|CA|=$\sqrt{(3-1)^{2}+(1-2)^{2}}$=$\sqrt{5}$,
∴最短的弦长为2$\sqrt{25-5}$=4$\sqrt{5}$.
故答案为4$\sqrt{5}$.
点评 本题主要考查直线过定点问题,直线和圆的位置关系,勾股定理,属于中档题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
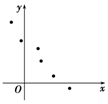
| A. | $\stackrel{∧}{y}$=1.5x+2 | B. | $\stackrel{∧}{y}$=-1.5x+2 | C. | $\stackrel{∧}{y}$=1.5x-2 | D. | $\stackrel{∧}{y}$=-1.5x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥$\sqrt{3}$ | B. | m≤$\sqrt{3}$ | C. | m≤-$\sqrt{3}$ | D. | -$\sqrt{3}$≤m≤$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{3}{5}$ | C. | ∁UA∩∁UB | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com