练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．假如你家订了一份报纸，送报人可能在早上6：30～7：30之间把报纸送到你家，你父亲离开家去工作的时间在早上7：00～8：00之间，记“你父亲在离开家前能得到报纸”为事件A，求事件A发生的概率．

    分析 根据题意，设送报人到达的时间为X，小明父亲离家去工作的时间为Y；则（X，Y）可以看成平面中的点，分析可得由试验的全部结果所构成的区域并求出其面积，同理可得事件A所构成的区域及其面积，由几何概型公式，计算可得答案．

    解答 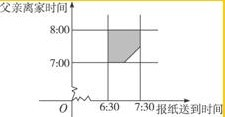解：设送报人到达的时间为X，小明父亲离家去工作的时间为Y，
    以横坐标表示报纸送到时间，以纵坐标表示父亲离家时间，建立平面直角坐标系，父亲在离开家前能得到报纸的事件构成区域是下图：
     由于随机试验落在方形区域内任何一点是等可能的，所以符合几何概型的条件．
    根据题意，只要点落到阴影部分，就表示父亲在离开家前能得到报纸，即事件A发生，
    所以P（A）=$\frac{1-\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}{1}$=$\frac{7}{8}$．

    点评 本题考查几何概型的计算，解题的关键在于设出X、Y，将（X，Y）以及事件A在平面直角坐标系中表示出来．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．圆（x+1）2+（y-4）2=25被直线4x-3y-4=0截得的弦长是（　　）
    A．3B．4C．6D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=ax3+bx2-3x（a，b∈R），曲线y=f（x）在点（1，f（1））处的切线方程为y+2=0
    （1）求函数f（x）的解析式
    （2）当x∈[-3，2]时，求f（x）的最大值和最小值
    （3）过点M（2，2）作曲线y=f（x）的切线l，求切线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知函数$f（x）=\left\{\begin{array}{l}（{2-a}）x-\frac{a}{2}，（{x＜1}）\\{log_a}x，（{x≥1}）\end{array}\right.$是R上的增函数，那么实数a的取值范围是[$\frac{4}{3}$，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知数列{an}，{bn}满足：a1=$\frac{1}{4}$，an+bn=1，bn+1=$\frac{{b}_{n}}{1-{{a}_{n}}^{2}}$
    （1）证明：{$\frac{1}{{b}_{n}-1}$}是等差数列，并求数列{bn}的通项公式；
    （2）设Sn=a1a2+a2a3+a3a4+…+anan+1，不等式4aSn＜bn对任意的n∈N*恒成立，求实数a的取值范围；
    （3）是否存在正整数m，k，使（$\frac{1}{{a}_{k}}$-2）2=（$\frac{1}{{a}_{m}}$-3）（$\frac{1}{{a}_{m}}$-2）+19成立？若存在，求出m，k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设曲线$y=\frac{2}{x-1}$在点（3，1）处的切线与直线ax-y+1=0垂直，则a=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．正项数列{an}的前n项和为sn，且$2\sqrt{s_n}={a_n}+1$．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设${b_n}={a_n}•{2^{{a_n}+1}}$，数列{bn}的前n项和为Tn，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．以直角坐标系xOy的原点为极点，x轴的正半轴为极轴，且两坐标系取相同的长度单位，已知点N的极坐标为（2，$\frac{π}{2}$），M是曲线C：p2•（cos2θ-sin2θ）+1=0上任意一点，点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+$\overrightarrow{ON}$，设点P的轨迹为曲线Q．
    （1）求曲线Q的直角坐标方程；
    （2）若直线l：$\left\{\begin{array}{l}{x=-2-t}\\{y=2-\sqrt{3}t}\end{array}\right.$（t为参数）与曲线Q的交点为A、B，求|AB|的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知数集A={a1，a2，…，an}（1≤a1＜a2＜…an，n≥2）具有性质P；对任意的i，j（1≤i≤j≤n），aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A．
    （1）分别判断数集{1，3，4}与{1，2，3，6}是否具有性质P，并说明理由；
    （2）证明：a1=1，且$\frac{{{a_1}+{a_2}+…+{a_n}}}{{a_1^{-1}+a_2^{-1}+…+a_n^{-1}}}={a_n}$；
    （3）当n=5时，若a2=2，求集合A．

    查看答案和解析>>

    同步练习册答案