
【题目】
有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为![]() .
.
(Ⅰ)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(Ⅱ)若四名运动员每两人之间进行一场比赛,设甲获胜场次为![]() ,求随机变量
,求随机变量![]() 的分布列及期望
的分布列及期望![]() .
.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若函数
,若函数![]() 满足:对于给定的
满足:对于给定的![]()
![]() ,存在
,存在![]() ,使得
,使得![]() 成立,那么称
成立,那么称![]() 具有性质
具有性质![]() .
.
(1)函数![]()
![]() 是否具有性质
是否具有性质![]() ?说明理由;
?说明理由;
(2)已知函数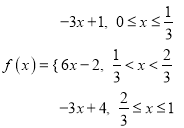 具有性质
具有性质![]() ,求
,求![]() 的最大值;
的最大值;
(3)已知函数![]() 的定义域为
的定义域为![]() ,满足
,满足![]() ,且
,且![]() 的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数
的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数![]() 具有性质
具有性质![]() ,若存在,求出这样的n的取值集合;若不存在,请说明理由.
,若存在,求出这样的n的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知含有![]() 个元素的正整数集
个元素的正整数集![]() (
(![]() ,
, ![]() )具有性质
)具有性质![]() :对任意不大于
:对任意不大于![]() (其中
(其中![]() )的正整数
)的正整数![]() ,存在数集
,存在数集![]() 的一个子集,使得该子集所有元素的和等于
的一个子集,使得该子集所有元素的和等于![]() .
.
(Ⅰ)写出![]() ,
, ![]() 的值;
的值;
(Ⅱ)证明:“![]() ,
, ![]() ,…,
,…, ![]() 成等差数列”的充要条件是“
成等差数列”的充要条件是“![]() ”;
”;
(Ⅲ)若![]() ,求当
,求当![]() 取最小值时
取最小值时![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的学生中随机选出100名女生并统计她们的身高(单位: ![]() ),得到如图频率分布表:
),得到如图频率分布表:
分组(身高) |
|
|
|
|
(Ⅰ)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 的女生应抽取几人?
的女生应抽取几人?
(Ⅱ)在(Ⅰ)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,若将f(x)的图象上所有点向右平移
)的部分图象如图所示,若将f(x)的图象上所有点向右平移 ![]() 个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( ) 
A.![]() ,k∈Z
,k∈Z
B.![]() ,k∈Z
,k∈Z
C.![]() ,k∈Z
,k∈Z
D.![]() ,k∈Z
,k∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆![]() 上有四个不同的点到直线
上有四个不同的点到直线![]() 的距离为2,则
的距离为2,则![]() 的取值范围是( )
的取值范围是( )
A. (-12,8) B. (-8,12) C. (-13,17) D. (-17,13)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com