
【题目】如图,在四棱锥O﹣ABCD中,OA⊥底面ABCD,且底面ABCD是边长为2的正方形,且OA=2,M,N分别为OA,BC的中点.
(1)求证:直线MN![]() 平面OCD;
平面OCD;
(2)求点B到平面DMN的距离.

科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.

(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() 两点,且圆心C在直线
两点,且圆心C在直线![]() 上.
上.
(1)求圆C的方程;
(2)设![]() ,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使
,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使![]() 是常数,若存在,求出点N坐标;若不存在,说明理由.
是常数,若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,g(x)=
,g(x)=![]() (a>0,且a≠1).
(a>0,且a≠1).
(1)求函数φ(x)=f(x)+g(x)的定义域;
(2)试确定不等式f(x)≤g(x)中x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是y=f(x)导函数的图象,对于下列四个判断:
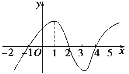
①f(x)在[-2,-1]上是增函数;
②x=-1是f(x)的极小值点;
③f(x)在[-1,2]上是增函数,在[2,4]上是减函数;
④x=3是f(x)的极小值点.
其中判断正确的是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,当直线
,当直线![]() 的倾斜角是
的倾斜角是![]() 时,
时, ![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() .
.

(1)求![]() 的值;
的值;
(2)以![]() 为直径的圆交
为直径的圆交![]() 轴于点
轴于点![]() ,记劣弧
,记劣弧![]() 的长度为
的长度为![]() ,当直线
,当直线![]() 绕
绕![]() 点旋转时,求
点旋转时,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com