
【题目】已知 ![]() ,记关于
,记关于 ![]() 的不等式
的不等式 ![]() 的解集为
的解集为 ![]() .
.
(1)若 ![]() ,求实数
,求实数 ![]() 的取值范围;
的取值范围;
(2)若 ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】一直函数![]() ,其中
,其中![]()
(1)讨论![]() 的单调性
的单调性
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,曲线在点
,曲线在点![]() 处的切线方程为
处的切线方程为![]() ,求证:对于任意的正实数
,求证:对于任意的正实数![]() ,都有
,都有![]()
(3)若关于![]() 的方程
的方程![]() (
(![]() 为实数)有两个正实根
为实数)有两个正实根![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=![]() )
)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C: ![]() +
+ ![]() =1,直线l:
=1,直线l: ![]() (t为参数)
(t为参数)
(1)写出曲线C的参数方程,直线l的普通方程.
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
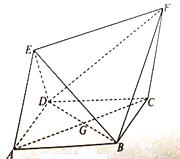
【题目】如图,四边形 ![]() 为菱形,四边形
为菱形,四边形 ![]() 为平行四边形,设
为平行四边形,设 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,
, ![]() .
.
(1)证明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() 与平面
与平面 ![]() 所成角为60°,求二面角
所成角为60°,求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)的函数f(x),其导函数为f′(x),满足:f(x)>0且 ![]() 总成立,则下列不等式成立的是( )
总成立,则下列不等式成立的是( )
A.e2e+3f(e)<e2ππ3f(π)
B.e2e+3f(π)>e2ππ3f(e)
C.e2e+3f(π)<e2ππ3f(e)
D.e2e+3f(e)>e2ππ3f(π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,以x轴的正半轴为极轴建立极坐标系.设曲线C的参数方程为 ![]() (α是参数),直线l的极坐标方程为ρcos(θ+
(α是参数),直线l的极坐标方程为ρcos(θ+ ![]() )=2
)=2 ![]() .
.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1. 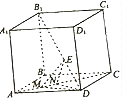
⑴当N为对角线AC的中点且DE= ![]() 时,则三棱锥E﹣DMN的体积是;
时,则三棱锥E﹣DMN的体积是;
⑵当三棱锥E﹣DMN的体积为 ![]() 时,则DE= .
时,则DE= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 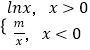 ,若f(x)﹣f(﹣x)=0有四个不同的根,则m的取值范围是( )
,若f(x)﹣f(﹣x)=0有四个不同的根,则m的取值范围是( )
A.(0,2e)
B.(0,e)
C.(0,1)
D.(0, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com