
ЁОЬтФПЁПШ§ЙњЪБДњЮтЙњЪ§бЇМведЫЌЫљзЂЁЖжмїТЫуОЁЗжаИјГіСЫЙДЙЩЖЈРэЕФОјУюжЄУїЃЌЯТУцЪЧедЫЌЕФЯвЭММАзЂЮФЃЌЯвЭМЪЧвЛИівдЙДЙЩжЎЯвЮЊБпЕФе§ЗНаЮЃЌЦфУцЛ§ГЦЮЊЯвЪЕЃЌЭМжаАќКЌЫФИіШЋЕШЕФЙДЙЩаЮМАвЛИіаЁе§ЗНаЮЃЌЗжБ№ЭПГЩКьЃЈжьЃЉЩЋМАЛЦЩЋЃЌЦфУцЛ§ГЦЮЊжьЪЕЁЂЛЦЪЕЃЌРћгУ2ЁСЙДЁСЙЩ+ЃЈЙЩЃЙДЃЉ2=4ЁСжьЪЕ+ЛЦЪЕ=ЯвЪЕЃЌЛЏМђЕУЙД2+ЙЩ2=Яв2ЃЌЩшЙДЙЩаЮжаЙДЙЩБШЮЊ![]() ЃЌШєЯђЯвЭМФкЫцЛњХзжР1000ПХЭМЖЄЃЈДѓаЁКіТдВЛМЦЃЉЃЌдђТфдкЛЦЩЋЭМаЮФкЕФЭМЖЄЪ§ДѓдМЮЊЃЈ ЃЉ
ЃЌШєЯђЯвЭМФкЫцЛњХзжР1000ПХЭМЖЄЃЈДѓаЁКіТдВЛМЦЃЉЃЌдђТфдкЛЦЩЋЭМаЮФкЕФЭМЖЄЪ§ДѓдМЮЊЃЈ ЃЉ
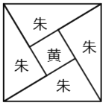
A.134B.866C.300D.188

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊзМШЗАбЮеЪаГЁЙцТЩЃЌФГЙЋЫОЖдЦфЫљЪєЩЬЦЗЪлМлНјааЪаГЁЕїВщКЭФЃаЭЗжЮіЃЌЗЂЯжИУЩЬЦЗвЛФъФкУПМўЕФЪлМлАДдТНќЫЦГЪ![]() ЕФФЃаЭВЈЖЏЃЈ
ЕФФЃаЭВЈЖЏЃЈ![]() ЮЊдТЗнЃЉЃЌвбжЊ3дТЗнУПМўЪлМлДяЕНзюИп90дЊЃЌжБЕН7дТЗнУПМўЪлМлБфЮЊзюЕЭ50дЊ.дђИљОнФЃаЭПЩжЊдк10дТЗнУПМўЪлМлдМЮЊ_____.ЃЈНсЙћБЃСєећЪ§ЃЉ
ЮЊдТЗнЃЉЃЌвбжЊ3дТЗнУПМўЪлМлДяЕНзюИп90дЊЃЌжБЕН7дТЗнУПМўЪлМлБфЮЊзюЕЭ50дЊ.дђИљОнФЃаЭПЩжЊдк10дТЗнУПМўЪлМлдМЮЊ_____.ЃЈНсЙћБЃСєећЪ§ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃЌжБЯп
ЃЌжБЯп![]() гыХзЮяЯпНЛгк
гыХзЮяЯпНЛгк![]() СНЕу.
СНЕу.
ЃЈЂёЃЉШє![]() ЃЌЧѓвд
ЃЌЧѓвд![]() ЮЊжБОЖЕФдВБЛ
ЮЊжБОЖЕФдВБЛ![]() жсЫљНиЕУЕФЯвГЄЃЛ
жсЫљНиЕУЕФЯвГЄЃЛ
ЃЈЂђЃЉЗжБ№Й§Еу![]() зїХзЮяЯп
зїХзЮяЯп![]() ЕФЧаЯпЃЌСНЬѕЧаЯпНЛгкЕу
ЕФЧаЯпЃЌСНЬѕЧаЯпНЛгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() УцЛ§ЕФзюаЁжЕ.
УцЛ§ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕЃЌНЋЧњЯп![]() ЩЯЕФУПвЛИіЕуЕФКсзјБъБЃГжВЛБфЃЌзнзјБъЫѕЖЬЮЊдРДЕФ
ЩЯЕФУПвЛИіЕуЕФКсзјБъБЃГжВЛБфЃЌзнзјБъЫѕЖЬЮЊдРДЕФ![]() ЃЌЕУЕНЧњЯп
ЃЌЕУЕНЧњЯп![]() ЃЌвдзјБъдЕу
ЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ ![]() жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌ
жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌ ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓЧњЯп![]() ЕФВЮЪ§ЗНГЬЃЛ
ЕФВЮЪ§ЗНГЬЃЛ
ЃЈЂђЃЉЙ§дЕу![]() ЧвЙигк
ЧвЙигк![]() жсЖдГЦЕФСНЬѕжБЯп
жсЖдГЦЕФСНЬѕжБЯп![]() гы
гы![]() ЗжБ№НЛЧњЯп
ЗжБ№НЛЧњЯп![]() гк
гк![]() ЁЂ
ЁЂ![]() КЭ
КЭ![]() ЁЂ
ЁЂ![]() ЃЌЧвЕу
ЃЌЧвЕу![]() дкЕквЛЯѓЯоЃЌЕБЫФБпаЮ
дкЕквЛЯѓЯоЃЌЕБЫФБпаЮ![]() ЕФжмГЄзюДѓЪБЃЌЧѓжБЯп
ЕФжмГЄзюДѓЪБЃЌЧѓжБЯп![]() ЕФЦеЭЈЗНГЬЃЎ
ЕФЦеЭЈЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌCDЁЮABЃЌ
жаЃЌCDЁЮABЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌEЪЧ
ЃЌEЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
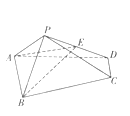
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓPЕНЦНУц![]() ЕФОрРы.
ЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌНЧAЃЌBЃЌCЫљЖдЕФБпЗжБ№ЮЊaЃЌbЃЌcЃЌЧвТњзуbcosAЉ![]() asinBЃН0ЃЎ
asinBЃН0ЃЎ
ЃЈ1ЃЉЧѓAЃЛ
ЃЈ2ЃЉвбжЊaЃН2![]() ЃЌBЃН
ЃЌBЃН![]() ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпC:x24pyЃЈpЮЊДѓгк2ЕФжЪЪ§ЃЉЕФНЙЕуЮЊFЃЌЙ§ЕуFЧваБТЪЮЊk(k0)ЕФжБЯпНЛCгкAЃЌBСНЕуЃЌЯпЖЮABЕФДЙжБЦНЗжЯпНЛyжсгкЕуEЃЌХзЮяЯпCдкЕуAЃЌBДІЕФЧаЯпЯрНЛгкЕуG.МЧЫФБпаЮAEBGЕФУцЛ§ЮЊS.
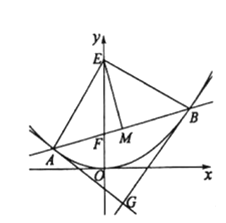
ЃЈ1ЃЉЧѓЕуGЕФЙьМЃЗНГЬЃЛ
ЃЈ2ЃЉЕБЕуGЕФКсзјБъЮЊећЪ§ЪБЃЌSЪЧЗёЮЊећЪ§ЃПШєЪЧЃЌЧыЧѓГіЫљгаТњзуЬѕМўЕФSЕФжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЩњВњФГжжЕчзгВњЦЗЃЌУПМўВњЦЗВЛКЯИёЕФИХТЪОљЮЊ![]() ЃЌЯжЙЄГЇЮЊЬсИпВњЦЗЩљгўЃЌвЊЧѓдкНЛИЖгУЛЇЧАУПМўВњЦЗЖМЭЈЙ§КЯИёМьбщЃЌвбжЊИУЙЄГЇЕФМьбщвЧЦївЛДЮзюЖрПЩМьбщ
ЃЌЯжЙЄГЇЮЊЬсИпВњЦЗЩљгўЃЌвЊЧѓдкНЛИЖгУЛЇЧАУПМўВњЦЗЖМЭЈЙ§КЯИёМьбщЃЌвбжЊИУЙЄГЇЕФМьбщвЧЦївЛДЮзюЖрПЩМьбщ![]() МўИУВњЦЗЃЌЧвУП МўВњЦЗМьбщКЯИёгыЗёЯрЛЅЖРСЂЃЎШєУПМўВњЦЗОљМьбщвЛДЮЃЌЫљашМьбщЗбгУНЯЖрЃЌИУЙЄГЇЬсГівдЯТМь бщЗНАИЃКНЋВњЦЗУП
МўИУВњЦЗЃЌЧвУП МўВњЦЗМьбщКЯИёгыЗёЯрЛЅЖРСЂЃЎШєУПМўВњЦЗОљМьбщвЛДЮЃЌЫљашМьбщЗбгУНЯЖрЃЌИУЙЄГЇЬсГівдЯТМь бщЗНАИЃКНЋВњЦЗУП![]() Иі
Иі![]() вЛзщНјааЗжзщМьбщЃЌШчЙћФГвЛзщВњЦЗМьбщКЯИёЃЌдђЫЕУїИУзщФкВњЦЗОљКЯИёЃЌШєМьбщВЛКЯИёЃЌдђЫЕУїИУзщФкгаВЛКЯИёВњЦЗЃЌдйЖдИУзщФкУПвЛМўВњЦЗЕЅЖРНјааМьбщЃЌШчДЫЃЌУПвЛзщВњЦЗжЛашМьбщ
вЛзщНјааЗжзщМьбщЃЌШчЙћФГвЛзщВњЦЗМьбщКЯИёЃЌдђЫЕУїИУзщФкВњЦЗОљКЯИёЃЌШєМьбщВЛКЯИёЃЌдђЫЕУїИУзщФкгаВЛКЯИёВњЦЗЃЌдйЖдИУзщФкУПвЛМўВњЦЗЕЅЖРНјааМьбщЃЌШчДЫЃЌУПвЛзщВњЦЗжЛашМьбщ![]() ДЮЛђ
ДЮЛђ![]() ДЮЃЎЩшИУЙЄГЇЩњВњ
ДЮЃЎЩшИУЙЄГЇЩњВњ![]() МўИУВњЦЗЃЌМЧУПМўВњЦЗЕФЦНОљМьбщДЮ Ъ§ЮЊ
МўИУВњЦЗЃЌМЧУПМўВњЦЗЕФЦНОљМьбщДЮ Ъ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФЗжВМСаМАЦфЦкЭћЃЛ
ЕФЗжВМСаМАЦфЦкЭћЃЛ
ЃЈ2ЃЉЃЈiЃЉЪдЫЕУїЃЌЕБ![]() дНаЁЪБЃЌИУЗНАИдНКЯРэЃЌМДЫљашЦНОљМьбщДЮЪ§дНЩйЃЛ
дНаЁЪБЃЌИУЗНАИдНКЯРэЃЌМДЫљашЦНОљМьбщДЮЪ§дНЩйЃЛ
ЃЈiiЃЉЕБ![]() ЪБЃЌЧѓЪЙИУЗНАИзюКЯРэЪБ
ЪБЃЌЧѓЪЙИУЗНАИзюКЯРэЪБ![]() ЕФжЕМА
ЕФжЕМА![]() МўИУВњЦЗЕФЦНОљМьбщДЮЪ§ЃЎ
МўИУВњЦЗЕФЦНОљМьбщДЮЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() .
.
ЃЈ1ЃЉЬжТлКЏЪ§_f(x)ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШє ![]() ЃЌЧв
ЃЌЧв![]() га2 ИіВЛЭЌЕФМЋжЕЕу
га2 ИіВЛЭЌЕФМЋжЕЕу![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com